www.mathematik-verstehen.de	https://mathe.web.leuphana.de	© Prof. Dr. Dörte Haftendorn
https://mathe.web.leuphana.de/analysis/polar/rosetten/rosetten.htm [Kurven] [Analysis] [Polarkoordinaten] [Polar-Kartesisch] [GeoGebra] [MuPAD]

Spiralen


Archimedische Spirale	Archimedische Spirale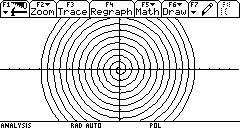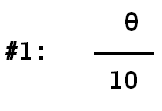
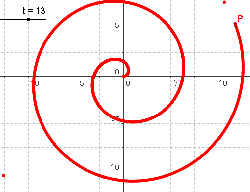Wurzel- Spirale	Wurzelspirale
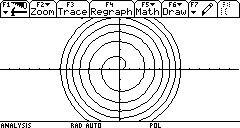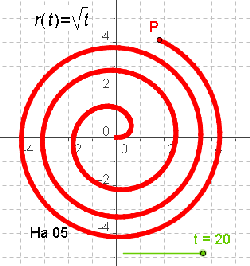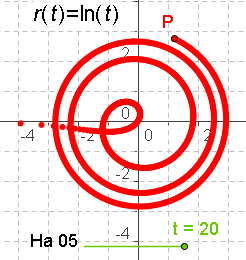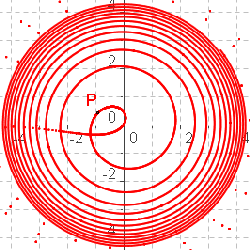Logarithmus- Spirale	Achtung: Ich bezeichne die Spiralen nach dem Funktionstyp von r(theta). Da hier r(theta)=ln(theta) ist, sage ich Logarithmus-Spirale oder auch logarithmische Spirale. Leider wird oft die Spirale aus dem nächsten Beispiel so bezeichnet. Logarithmus-Spirale
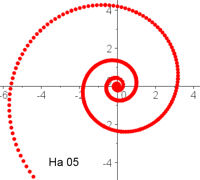
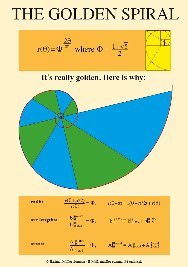
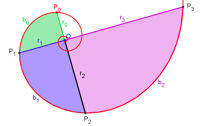
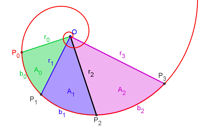
Exponential- Spirale = "logarithmische Spirale"	Exponential-Spirale r(theta)=a^(k theta) Achtung! diese wird häufig als "logarithmische Spirale" bezeichnet. Dieser Spiraltyp ist besonders geeignet, um Längenverhältnisse und Flächenverhältnisse mit Analysis-Methoden zu erkunden. Eine Besonderheit ergibt sich, wenn die Basis der Goldene Schnitt PHI ist. Goldene SpiraleAuf der Tagung der GDM 2011 in Freiburg hat StD Hartmut Müller-Sommer ein schönes Poster über die Goldene Spirale präsentiert. Sie ist in Polarkoordinaten gegeben durch gegeben durch Das hat mich angeregt, sie zu untersuchen und mit der Goldenen Schnecke zu vergleichen. Die multikativen Eigenschaften dieser durch eine Exponentialfunktion gegebenen Spirale finden sich in leicht abgewandelter Form bei allen Exponential-Spiralen und lassen sich leicht mit analytischen Methoden zeigen.. (Warum man diese meist "Logarithmische Spiralen" nennt, ist mir ein Rätsel.) Aber die additiven Eigenschaften gelten nur, weil Phi der Goldene Schnitt ist. Das alles ist im Folgenden ausgeführt: Die Goldene Spirale und ihre Eigenschaften Interaktive Erkundung der Goldenen Spirale bezüglich Radien und Bogenlängen Interaktive Erkundung der Goldenen Spirale bezüglich Sektorflächen Weiteres, insbesondere ein Vergleich mit der Goldenen Schnecke Schier unerschöpfliche weitere Untersuchnungen von Prof. Dr. Dieter Riebesehl, Leuphana Universität Lüneburg: Spiralen-Korrespondenz und Übersichtsbilder der nachfolgenden Dateien Logarithmische Spirale mit Kreisen Logarithmische Spirale mit Kreisen Mathematica-Datei dazu in pdf download Spiralen in Quadraten Spiralen in Quadraten Rechnungsgrundlage dazu Spirale auf dem DIN-A4-Blatt Spirale in Dreiecken