www.mathematik-verstehen.de
https://mathe.web.leuphana.de/analysis/polar/rosetten/rosetten.htm[Kurven] [Analysis] [Polarkoordinaten] [Polar-Kartesisch] [GeoGebra] [MuPAD]
| [Als höhere Kurven] | Gleichung | Bogenlänge,Fläche | Aufgaben | Konchoide der Rosette |
| Rosetten | 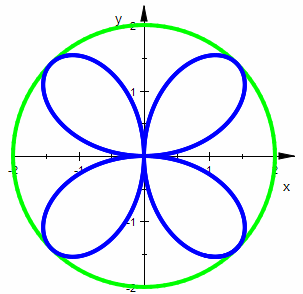 Kurven, die in einem intuitiven Sinn wie Rosetten, wie runde Blüten ausssehen, sollen hier Rosetten heißen. Damit ist also nicht in mathematisch strengen Sinn eine Kurvenklasse gemeint.Spricht jemand von der Rosette, dann wird er die vierblättrige durch r=a*sin(2t) vermittelte Kurve meinen, die in einen Kreis mit dem Radius a einbeschrieben ist, gleichwertig zu r=a*cos(2t) Sie eignet sich auch sehr gut zur Einführung, evt. nach den Spiralen, denn es bieten sich interessante Betrachtungen über den Durchlaufsinn an. Siehe Vortrag zu Polarkoordinaten besser verstehen   und entsprechende Seite zu Polar-kartesischer Koppelung  |
| Gleichungen | Kartesische Gleichung Polargleichung  Beweis des Zusammenhangs 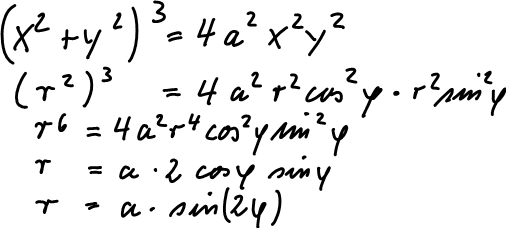 Hierzu unten die erste MuPAD-Datei in ihrer Mitte |
| Interaktiv mit GeoGebra |   Kreisblume download
|
| Interaktiv mit Euklid-Dynageo |
  Einführung mit sin(2t) download Nur Mit Internet-Explorersin(2t) mit Punkt-Sprung-Panne download |
| Rosette mit MuPAD |
 Rosette Einführung, dann mit Bogenlänge und Flächeninhalt
  
 Alte Version MuPAD 3  ohne Ausgaben download mit Ausgaben(1 MB)
Es existiert die uralte Version Mupad 2.5 Rosette Einführung, dann mit ihrer Konchoide, der Doppeleilinie
Alte Version MuPAD 3
|
| Erkundungs- Aufgabe |   Aufgabe, die ich 1997 für das Buch "Analysis-Aufgaben", das Günter Steinberg und Mechthid Ebenhöh herausgegeben haben, verfasst habe.Aufgabe: (kurz) Wo kommt der kleine Zipfel her?  |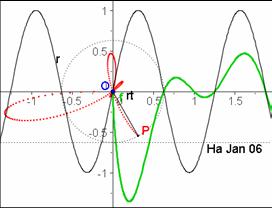
| Klausur- Aufgabe |  Schöne Aufgabe für eine Analysis-Klausur, gestellt im StaatsexamenGanze Klausur Dort auch Aufgabe zur Didaktik der Polarkoordinaten Polar-Blume polar+kartesisch |
| Konchoide der Rosette | 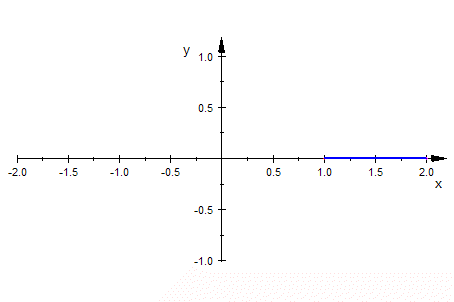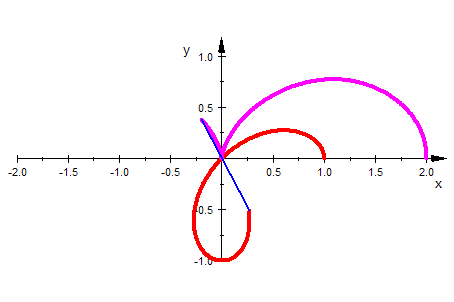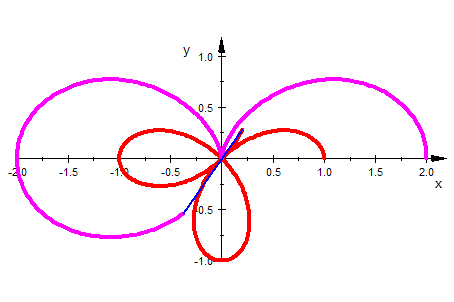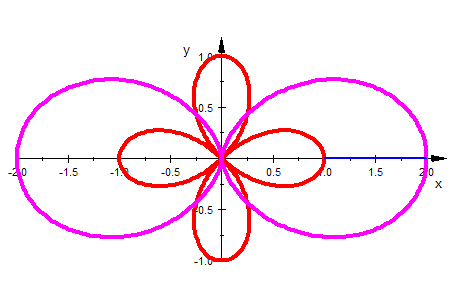 Eine Konchoide der Rosette ist die Doppel-Ei-LinieAusführliche Betrachtung Rosette Einführung, dann mit ihrer Konchoide, der Doppeleilinie |
|
[Kurven]
[Analysis]
[Polarkoordinaten]
[Polar-Kartesisch]
[GeoGebra]
[MuPAD]
| |||
 Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn Jan 2006, update | |||
|