www.mathematik-verstehen.de	https://mathe.web.leuphana.de	© Prof. Dr. Dörte Haftendorn
https://mathe.web.leuphana.de/analysis/polar/polar-kartes/polar-kartes.htm [Kurven] [Analysis] [Polarkoordinaten] [Polar-Kartesisch] [GeoGebra] [MuPAD]

Polarkoordinaten mit Kartesischer Koppelung

Polargleichung eines Kreises deuch den Ursprung mit Mittelpunkt(R,0) auf der x-Achse ist: r(phi)=2Rcos(phi). Herleitung hier.

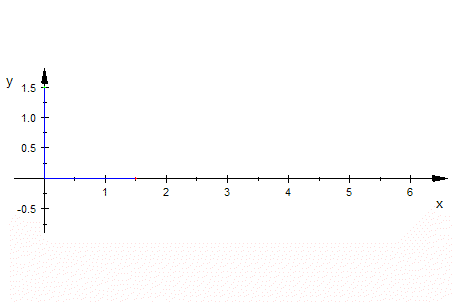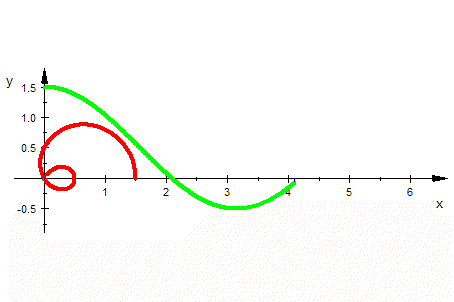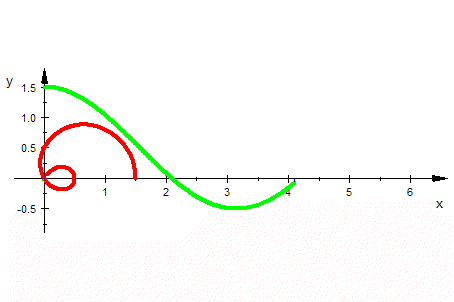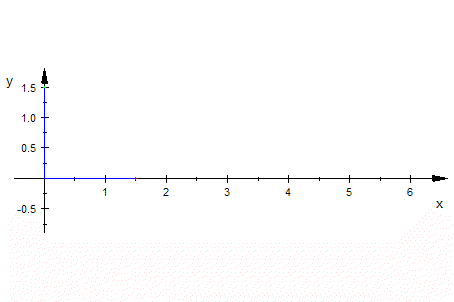
Was ist gemeint?	Polarkoordinaten besser verstehen durch bewegliche und gleichzeitige Darstellung der zugehörigen "kartesischen Funktion". 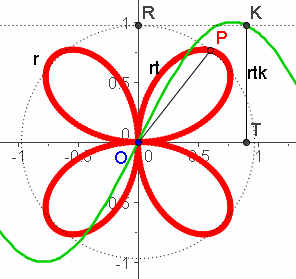Bei mathematischen Objekten, die in Polarkoordinaten dargestellt werden, ist es mitunter gar nicht so leicht zu sehen, wie sie bei wachsendem Winkel durchlaufen werden. Stellt man nun aber in derselben Zeichnung geometrisch gekoppelt zu P=(t, r(t)) polar auch P'=(t,r(t)) kartesisch dar, so entstehen zwei Ortskurven gleichzeitig, die eineindeutig aufeinander bezogen sind. So kann mit jeder vertrauten kartesischen Funktion eine entsprechende "Polarfunktion" erkundet werden. Besonders eignen sich DMS wie GeoGebra und CAS wie MuPAD 3. Von den heutigen Werkzeugen werden "Polarkoordinaten" angeboten und der Mathematikunterricht kann damit auf jedem Niveau von der 8. Klasse bis zum 8. Semester kreatives Mathematiklernen fördern. Achtung: seit GeoGebra zwei Grafik-Fenster nebeneinander gestattet, muss ich diese Seite heftig überarbeiten. Z.Z. sind die Dateien auf der Hauptseite "polar" besser. Daher bin ich dabei diese Seite aus dem Verkehr zu ziehen. Gehen Sie zur Hauptseite Polarkoordinaten
MuPAD 4 Animationen	polar-kartesische Darstellung, Ausführliche Untersuchungen mit allerlei Lerneffekten und animierten Graphen Alte Version Pascalsche Schecken in polar-kartesischer Darstellung polar-kartesische Darstellung der Kardioide Alte Version MuPAD 3
Inversion am Kreis	Genialer Zusammenhang mit diese Idee interaktiv erklärt
Inversion von Kurven	Pascalsche Schnecken und ihre Inversion am Kreis