www.mathematik-verstehen.de
[Kurven]
[Analysis]
[Polarkoordinaten]
[Polar-Kartesisch]
[Geometrie]
[Höhere Geometrie]
[Inversion]
[GeoGebra]
[MuPAD]
| Worum geht es? Pascalsche Schnecken  sind Hundekurven mit Kreisstraße. Sie sind spezielle Konchoiden
mehr zu Polarkoordinaten 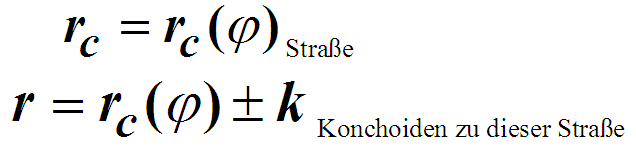 mehr zur Polar-kartesischen Doppel-Darstellung
Inverion am Kreis
Der Wanderkreis sei der Kreis um (1/2,0) mit dem Radius 1/2, die Polargleichung ist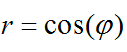 
Der "Baum" sei im Ursprung. Die Polargleichung der Pascalsche Schnecken ist dann: 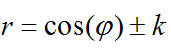 Inverse Objekte am Einheitskreis stellen sich algebraisch als das Konjugiert-Komplexe des algebraisch Inversen dar. Da der Kosinus aber eine gerade Funktion ist, muss man lediglich den Kehrwert bilden. Die Inversen der Pascalschen Schnecken haben also die Polargleichung 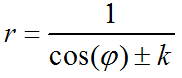 Und die Kegelschnitte haben die allgemeine Polargleichung 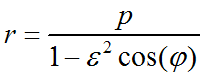 Da sieht man, dass gewisse Parameter der Kegelschnitte dazu passen. Die Bilder der Pascalschen Schnecken sind also Kegelschnitte. |
  Inversion der Pascalschen Schnecken  
|
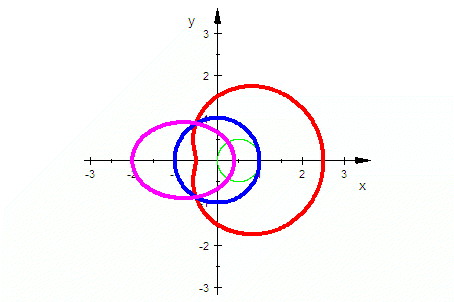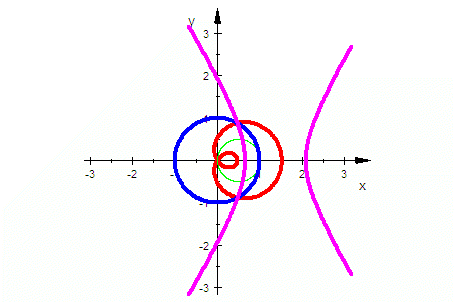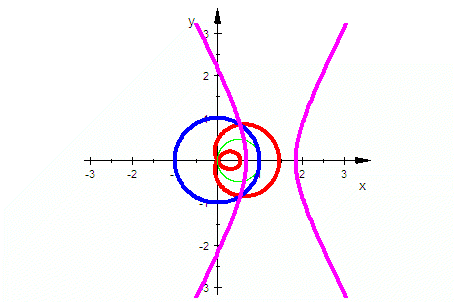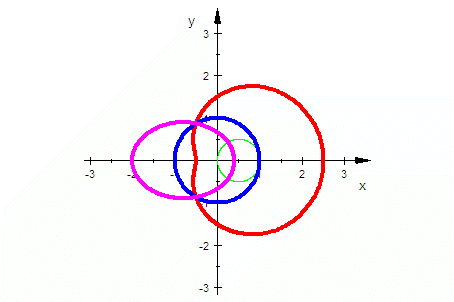Die nachfolgenden Bilder sind eigentlich nur in der schrittweisen Entstehung verständlich. Obige MuPAD-Dateien enthalten die Einzelteile übersichtlich. |
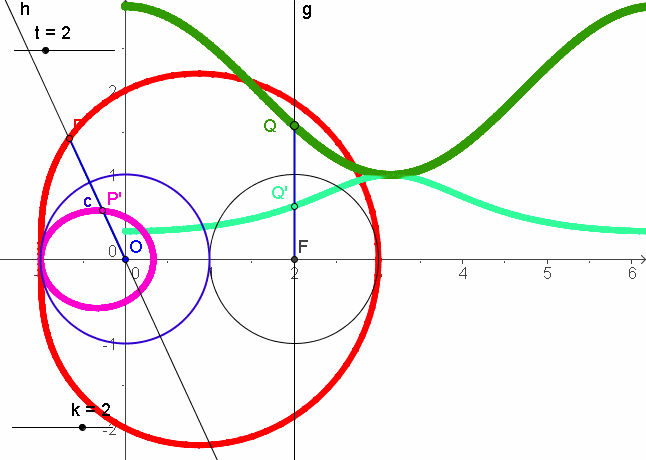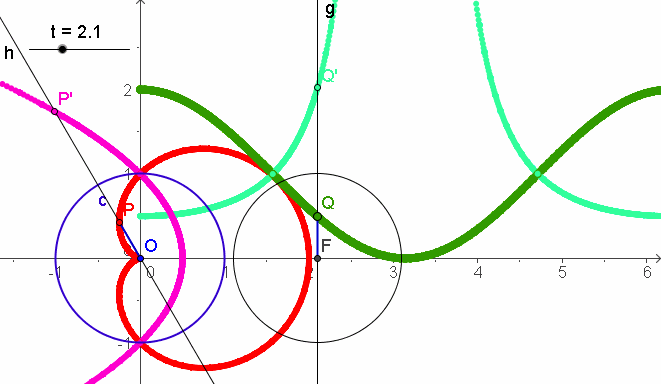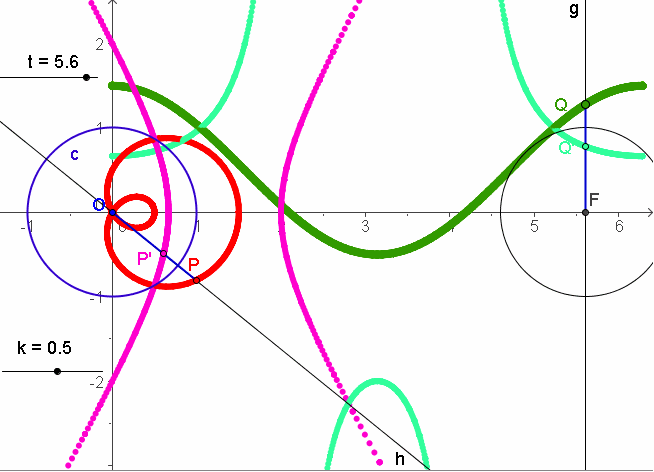 Stumpfe Schnecke ---- Ellipse download  |
Kardiode --- Parabel download |
Schnecke mit Schlaufe --- Hyperbel download |
| Kreis selbst --- Gerade download |
|
[Kurven]
[Analysis]
[Polarkoordinaten]
[Polar-Kartesisch]
[Geometrie]
[Höhere Geometrie]
[Inversion]
[GeoGebra]
[MuPAD]
| |||
 Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn Jan 2006, update | |||
|