www.mathematik-verstehen.de
haftendorn.uni-lueneburg.de/mathe-lehramt/kurven/hoehere/konchoiden/pascal.htm[Kurven] [Höhere] [Konchoiden] [Polarkoordinaten] [Polar-Kartesisch] [Inversion] [GeoGebra] [MuPAD]
Definition |
Grundlage |
Aufgabe von Hand |
Gleichungen, Polarkoordinaten |
Kardioide |
Katakaustik |
Inversion |
| Definition |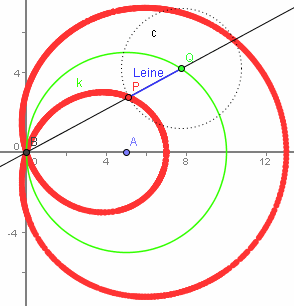 
Bei der allgemeinen Definition den Konchoiden es eine Kurve, genannt Straße, auf der ein Punkt Q (genannt Herrchen) läuft, und einen Punkt B, genannt Baum.
Q und B werden durch eine Gerade verbunden und auf dieser wird eine Strecke fester Länge k nach beiden Seiten abgetragen. Man kann die Endpunkte P bzw. P' deuten als Ort eines Hundes, der an an einer Leine fester Länge zu dem Baum strebt oder von ihm weg zerrt.Ist die Straße eine Gerade, dann ist die Ortskurve von P (des Hundes) eine Hundekurve .
Ist die Straße ein Kreis, dann ist die Ortskurve von P (des Hundes) eine allgemeine Kreiskonchoide .
Ist die Straße ein Kreis und steht der Baum auf dem Kreisrand, dann ist die Ortskurve von P (des Hundes) einePascalsche Schnecke. Die Form der Pascalschen Schnecken hängt noch von der Leinenlänge k im Vergleich zum Radius de "Wanderkreises" ab. Ist speziell die Leinenlänge k gleich dem Durchmesser des Wanderkreises, dann erhält man die Kardioide
Für eine rechnerische Behandlung ist es am einfachsten, wenn der Baum im Ursprung steht. |
|
| Grundlage |
 Pascalsche Schnecken    Pascalsche Schnecken  Pascalsche Schnecken in doppelter Ansicht Dieses ist möglich seit GeoGebra implizite kartsesiche Gleiungen zeichnen kann und dazu noch zwei Grafikfenster hat.(2011) Pascalsche Schnecken, Kreis links
Diese Stellung ist beim Thema Reflexion verwendet. |
|
| Aufgabe von Hand für Klausur |
 
Klassenarbeits- und Klausuraufgaben dieses Typs erlauben eine vertretbare Bearbeitung von Hand in Prüfungen und erlauben dennoch die am Computer im Unterricht gemachten Erfahrungen als Lernerfolg fruchtbar werden zu lassen. Weiteres dazu auf den Seiten zur Lehre algebraischer Kurven Rubrik Klausuren, Rasteraufgaben.Dieses Bearbeitungs-Bild in größerer Version Dieses Bearbeitungs-Bild in größerer Version gleich mit der Aufgabe |
|
| Gleichungen | 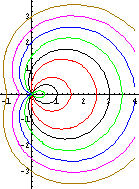 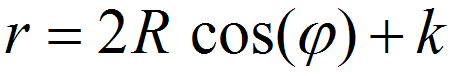 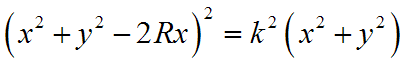 Dabei ist R der Radius des Wanderkreises und k die Leinenlänge. Pascalsche Schnecken Pascalsche Schnecken
 |
|
| in Polar-koordinaten | Pascalsche Schnecken in polar-karstesischer Darstellung   | |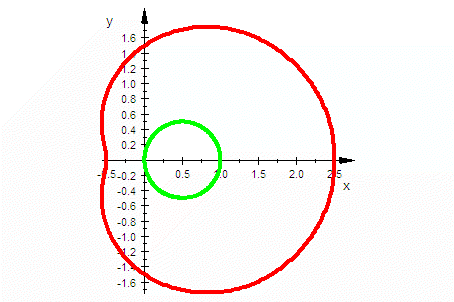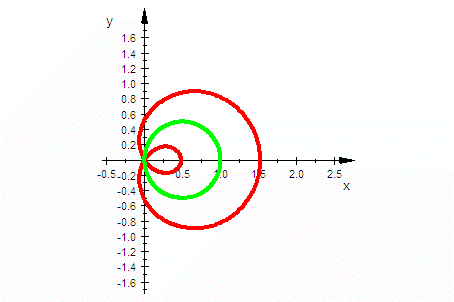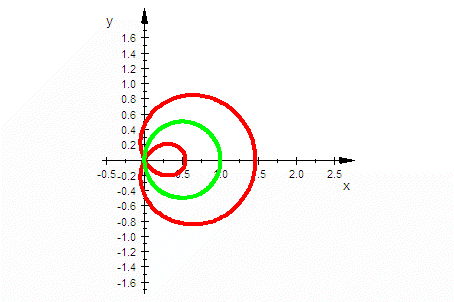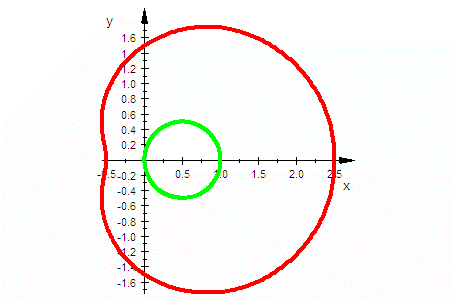
| Kardioide | Die Kardioide entsteht, wenn die Leinenlänge gleich dem Durchmesser des Wanderkreises ist, also für k=2R. Weiteres zur Kardioide im  Geschichtliches, Konstr.Beschreibung...Die Kardioide entsteht auch als Hüllkurve reflektierter Lichstrahlen, die von einem Punkt des Randes ausgehen. Man nennt Hüllkurven von Lichtstrahlen "Katakaustiken"
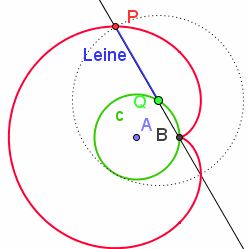
 Auch das Apfelmännchen 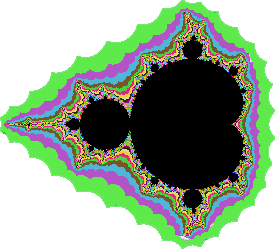 hat als Rand des Hauptkörpers eine Kardioide.
| |
| Inversion | 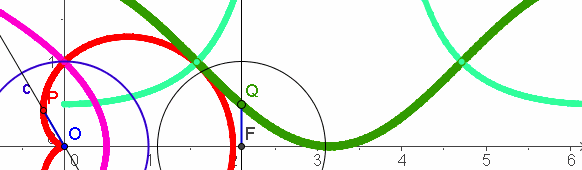 Invetriert man die Pascalschen Schnecken am Einheitskreis so entstehen erstaunlicherweise Kegelschnitte Extra Leitseite |
|
[Kurven]
[Höhere]
[Konchoiden]
[Polarkoordinaten]
[Polar-Kartesisch]
[Inversion]
[GeoGebra]
[MuPAD]
| |||
 Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn Juli 2005, update | |||
|
