[Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum] [Höhere Geometrie] [Probleme der Antike]
| Vortrag |
|
| Gezeigte Dateien und Weiterführungen |
|
| Thematik | Applets und Dateien | Didaktische Bemerkungen |
Reflexion an Geraden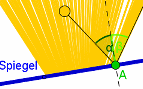 |
|
Die ersten beiden Dateien sind zum Erkunden geeignet. Die dritte macht nochmals das Ergebnis klar. |
Reflexion an der Parabel 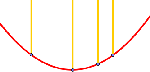 |
|
Zuerst wird die Reflexion konstruiert. Durch das Ziehen an P zeigen die reflektierten Strahlen dein Brennpunkt von alleine an. Dann lässt man sich durch Betrachtung der Feuerwehraufgabe anregeb, F zu spiegeln. Das macht dann die nächst Datei. So kann man die Leitgerade selbst entdecken. |
|
||
Reflexion an der Ellipse 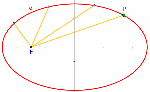 |
Das Vorgehen entspricht fast genau dem an der Parabel. Es ist hier zunächst F nicht der Brennpunkt, sondern irgendein Punkt auf der Achse. Das Verschieben von F bringt dann erst den Brennpunkt der Lichtstrahlen heraus. Dieser wird gespiegelt. Sein Ort ist dann der (hier unerwartete) Leitkreis. Wenn dann die Ellipse mit dem so entdeckten Leitkreis konstruiert wird, erhält man (überraschederweise) auch die Hyperbel. |
|
Reflexion an Kegelschnitte gemeinsame Sicht |
Dies sind etwas ältere Dateien, entstanden bevor es die Schaltkästchen gab. Daher gibt es die gestuften Versionen. Diese Dateien zeigen direkt die Phänomene, sie sind nicht diaktisch aufbereitet. Manmal braucht man aber auch solche, ohne viel "Drumrum". Inzwischen würde ich manche schöne machen, machen Sie's selbst. |
|
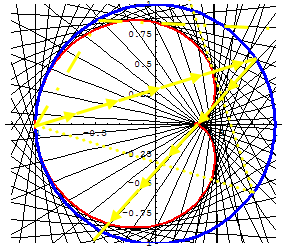
Katakaustik und Kardioide 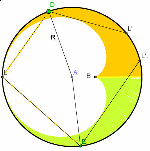 |
Hüllkuven von reflektierten Strahlen heißen Katakaustiken., wenn es sich um eine punktförmige Lichtquelle handelt. | |
|
||
Nephroide 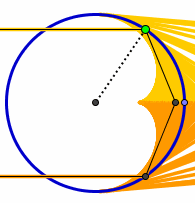 |
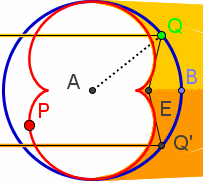 Hüllkuven von reflektierten Strahlen heißen Kaustiken., wenn es sich um parallel einfallendes Licht handelt. Hüllkuven von reflektierten Strahlen heißen Kaustiken., wenn es sich um parallel einfallendes Licht handelt.
|
|
Hundekurve und Lichtstrahlen  |
Eine Reflexion scheitert erstmal daran, dass die Tangenten nicht so einfach zu erzeugen sind. | |
http://haftendorn.uni-lueneburg.de http://mathematik.uni-lueneburg.de |