Mandelbrotmengen und Juliamengen


Das Apfelmännchen wohnt in der komplexen Zahlenebene. und c sind komplexe Zahlen. Grundlage ist die Gleichung

Start bei z_o. Die Folge z_o, z₁, z₂,... nennt man die Bahn (den Orbit) von z_o.
Gute Darstellung interaktiv mit GeoGebra ohne Bild *.ggb
Gute Darstellung interaktiv mit GeoGebra mit Bild *.ggb

Diese Folge kann man in ihrer Entstehung mit meinem Programm apfjulia © Ha94 beobachten.

Beim Apfelmännchen wird wird jeder Punkt als ein c aufgefaßt.

Apf5 Wenn dann die Bahn des Ursprungs nach N Schritten beschränkt bleibt, d.h. Abstand 2 vom Ursprung nicht überschreitet, dann wird c schwarz (blau) gefärbt. (Im rechten Bild weiß.) Sonst erhält c eine Farbe, die der Indexnummer entspricht, bei der dieser Abstand 2 überschritten wurde. N heißt Iterationstiefe.

Dabei entsteht das Apfelmännchen mit vielen Farben in der Nähe seines Randes. Im obersten Bild reicht die große Ellipse von -2 bis 1 und von -1,33 i bis +1,33 i .Also verläuft die imaginäre Achse etwa rechts neben der oberen und der unteren großen Knospe entlang. Die reelle Achse ist die Symmetrieachse.

Die anderen Bilder sind Ausschnitte. Dabei ist die Innenfarbe nun hellgrau statt blau.

Die Iterationstiefe war N=5000.

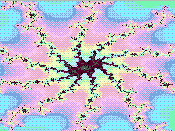Apf6a Apf6b Diese beiden Bilder haben den Bereich -0,52330750 + 0.68811162 i links unten -0.52330574 + 0.68811408 i rechts oben
Sie sind also nur 3 Millionstel breit und hoch. Hier zeigt sich, dass die Farben zwar beliebig sind, aber dennoch den Eindruck des Bildes stark beeinflussen. Punkte in einem zusammenhängenden Gebiet einer Farbe habe dieselbe "Fluchtgeschwindigkeit", der Orbit hat also bei derselben Iterationsnummer den Kreis mit Radius 2 verlassen.

Einschränkung auf reelle c

Wenn c reell ist, dann ist die Folge {0, c, c^2+c, ((c^2+c)^2+c),....} eine reelle iterationsfolge. diese kann man mit den Methoden der reellen Iteration und ihren Darstellungsmöglichkeiten untersuchen ( siehe Thema Rekursion

Verbale Erklärungen finden sich auch in meinem Buch im Bereich Fraktale, Mandelbrotmengen

Reelle Iteration

Weitere Beispiele

Apf2 Allgemeinere Mandelbrotmengen (benannt nach B. Mandelbrot) erhält man, wenn man als f(z) andere komlexe Funktionen wählt.
Beispiele sind in meinem Programm apfjulia © Ha94
Diese Bilder sind mit WinFract (s.u.) der Windowsversion des bekannten Fractint erstellt. Apf4

Sie können WinFrakt bei mir herunterladen.

Apfelmännchen, mit eigener Zoom-Möglichkeit
Eine schöne und sehr schnelle Software zum Zoomen in des Apfelmännchen hat Andreas Stiller 1998 in der Zeitschrift c't veröffenlicht. Ich habe hier ein kleines *.zip

. Packen Sie das aus und starten Sie ctapfw.exe. Beim Klicken erscheint das Apfelmännchen. Bei jedem weiteren Links-Klick wird die Klickstelle zum Mittelpunkt gemacht und hineingezoomt. Beim Rechtsklick geht es wieder hinaus. Links unten werden die Mauskoorinaten und die momentanen Mittelpunktskoordinaten angezeigt.
Dieses Programm iteriert etwa 100 Mio mal und erzeugt damit sehr schön feine Bilder. Siehe rechts.
Warum das Programm 3D im Namen hat, ist mir unklar.

Apfelmännchen, mit eigener Zoom-Möglichkeit
Internet in Griechenland http://www.softlab.ece.ntua.gr/miscellaneous/julia-apfel/
Anleitung: Stelle unter dem Bild ZoomFactor auf ZoomInx2 und klicke an einer interessanten Stelle in das Bild. Dann wird die Umgebung dees ausgewählten Punktes 2-fach vergrößert.
Diese Bilder sind nicht so gut wie die von obigem Proramm.

Das Buch Fraktale und Julia-Mengen Dufner, Julius /Roser, Andreas /Unseld, Frank:

Kartoniert / Harri Deutsch /BRO / 04.1998 / (ISBN 3-8171-1564-4) Euro 24,80
Hat eine sehr hilfreiche CD, bester Windowsstandard, mit vielen Möglichkeiten zur Interaktion und zur Erklärung. Der Text ist eher für Hochschule als für Schule geeignet, gibt aber dem Lehrer gsolide Informationen, wo Schüler Spannendes erforschen können.

[Fraktale (Leitseite)] [Programme]

(1996)(2002) Apr. 2005, update 21. Juni 2012

Direkte Internetadressen
[www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt]