www.mathematik-verstehen.de
[Graphen] [Folgen] [Weg-Fraktale] [Dimension] [IFS] [Mandel...] [Natur] [Dynamik] [Automaten] [Programme]
 |
RekursionEin tragfähiges Konzept für nachhaltigen Mathematikunterricht
|
 |
| Einführung Begriffe |
Warum Rekusion? |
Aufgaben Allgemeine Rekursion |
Explizite Folgen und ihre Grenzwerte |
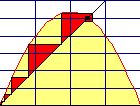
| Einführung |  Einführendes Beispiel kann ein möglichst handlungsorientiertes Problem sein, das auf eine "rekursive Formel" führt. Einführendes Beispiel kann ein möglichst handlungsorientiertes Problem sein, das auf eine "rekursive Formel" führt.Es eignet sich der Turm von Hanoi (3 Stangen, n Scheiben...) Man legt n+1 Scheiben um, indem man n Scheiben umlegt, dann die größte Scheibe platziert und dann wieden n Scheiben in an Schritten auf diese legt. Die rekursive Formel ergibt sich aus der Handlung. 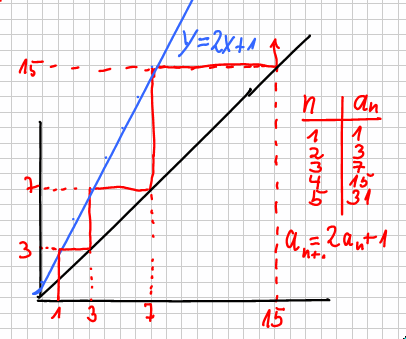 Die "Treppchen-Darstellung" wird daraus entwickelt. Vorgehen: Schreibe zu der rekursiven Formel die "entsprechende Trägerfunktion" auf (kurz Kurve genannt) und zeichne sie zusammen mit der Winkelhalbierenden (Wh). Mache dir klar, dass sich die Folgenwerte graphisch ergeben aus: Von Start zur nach oben zur Kurve Waagerecht zur Wh, senkrecht zur Kurve Waagerecht zur Wh, senkrecht zur Kurve und so weiter.... Die Lernenden machen erste Erfahrungen, Vokabeln: anziehender, b.z.w. abstoßender Fixpunkt, Einfluss des Startwertes, Abhängigkeit des Verhaltens von der Steigung, .... Ziel ist das Fazit |
| Interaktive Unterstützung der Einführung | Interaktive Möglichkeiten unterstützen das Verstehen
|
| Fazit |
Merksatz zur Rekursion allgemein, einige Fragen...
|
| Begriffe | Die Formeln mit denen man an+1 aus an berechnet heißen rekursive Formeln (lat: recurrere=zurücklaufen). Wenn man die Folgenwerte von einem Startwert ausgehend nacheinander berechnet, geht man iterativ vor (lat.:iterum=wiederum). Entsprechend sind Rekusion und Iteration verschiedene Sichtweisen auf dasselbe Problem. Ein wirklich rekursives Vorgehen ist für Computer auch möglich. Das kann man besonders gut bei den "Weg-Fraktalen und Lindemayersystemen" und bei den IFS-Fraktalen sehen. Bei den "Mandelbrot- und Juliamengen" und beim Lorenzattraktor (und Verwandten) geht man iterativ vor. |
| Anmerkung | Rekursion, die Darstellung mit Spinnwebgraphen und zugehöriges Feigenbaumdiagramm ist mit der logistischen Parabel eindrucksvoll und weit verbreitet. Es geht aber mit allen Kurvenscharen, die abhängig von einem Parameter die Winkelhalbierende verschieden steil schneiden. Hier sollen zuerst die Phänomene an dem Standardbeispiel "logistische Parabel" erkärt werden. Dann folgen Beispiele für allgemeinere Fälle. Das ganze, auch schulisch sehr relevante Thema Wachstum |
| Logistische Parabel |
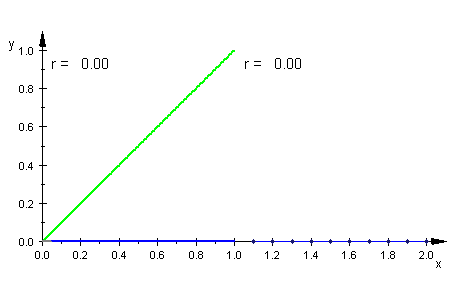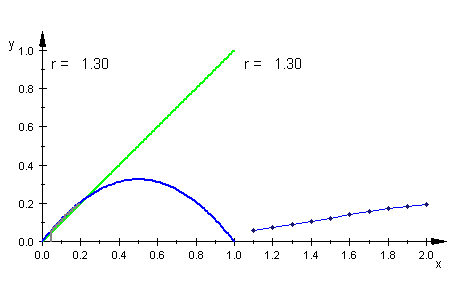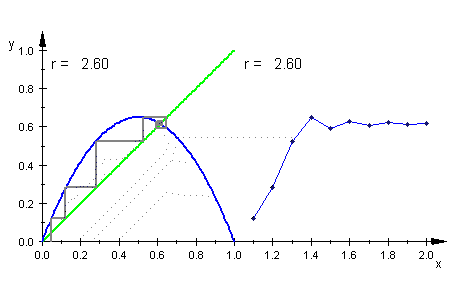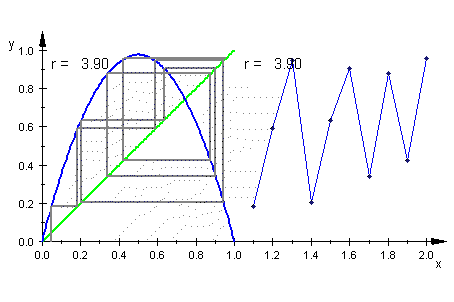 Aus der MuPAD-Datei Aus der MuPAD-Datei
geeignet zum interaktiven Erklären des Spinnwebverfahrens Dazu eine ausfürliche Erklärungs- und Aufgabenseite Über meine Seiten hinaus wird auch die "Schattenbahn" eingegangen. Darunter verstehen sie die Bahn bei nur wenig abweichenden Startwert. Es wird die Sensitivität demonstriert, die beiden Bahnen entwickeln sich schnetll auseinander. Es gibt dagen ein dagegen "Schattenbahn-Lemma", Peitgen nennt es "Beschattungs-Lemma" (Kap. 1.8 in "Chaos, Bausteine der Ordnung"), engl. shadow lemma. Es besagt, das es um jede evt. mit Rundungsfehlern behaftete Bahn einen Epsilonschlauch gibt mit der Eigenschaft, dass es in der Epsilonumgebung des Startwertes einen Startwert gibt, dessen Bahn wirklich ganz in dem Epsilonschlauch liegt. Diese Bahn heißt "Schattenbahn". Das Schattenbahn-Lemma hebelt die Kritik aus, dass man wegen der Rundungsfehler bei Gleitkommazahlen nicht die wahre Bahn sieht. |
| Feigenbaumdiagramm der Logistischen Parabel |
Didaktisch wertvoll ist die Umschaltbarkeit zwischen den üblichen Zeit-Graphen und der Spinnwebgraphen. Dazu ist auch die Betrachtung der Iterierten möglich. http://www.turboplot.de |
| Erste Aufgaben und Fragestellungen |
|
| Rekursion und Iteration allgemein |
geeignet zum interaktiven Erklären des Spinnwebverfahrens Dort auch der Beweis der superschnellen Konvergenz des Newtonverfahrens. |
Thesen Warum Rekursion? |
|
|