[Graphen] [Rekursion] [Weg-Fraktale] [Dimension] [IFS] [Mandel...] [Natur] [Dynamik] [Automaten] [Programme]
|
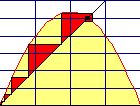
Rekursive FolgenSpinnweb-Darstellung und erste Erkenntnisse
|
Eine Folge heißt streng rekursiv, wenn gilt ![]() . Jedes gegebene a0 definiert zusammen mit der
rekursiven Formel eine neue Folge. f heißt Trägerfunktion der Folge.
. Jedes gegebene a0 definiert zusammen mit der
rekursiven Formel eine neue Folge. f heißt Trägerfunktion der Folge.
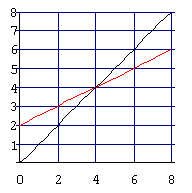 |
Startet man mit 0, so ergibt sich nacheinander 2, 3, 3.5, 3.75,..... |
|
|---|---|---|
| Übung oder Text zum Arbeitsblatt Webversion
Arbeitsblatt Zeichnen Sie sich etliche Geraden und Parabeln, die die Winkelhalbierende in verschiedenen Richtungen schneiden und experimentieren Sie mit verschiedenen Startpunkten. |
|
|
Gezeichnet sind auf der Übungsseite die Trägerfunktionen für entsprechende rekursiv definierte Folgen.
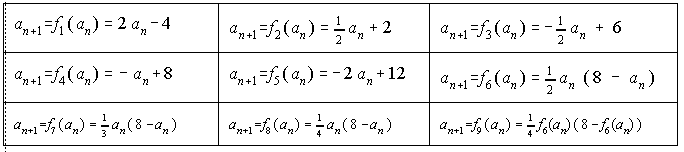
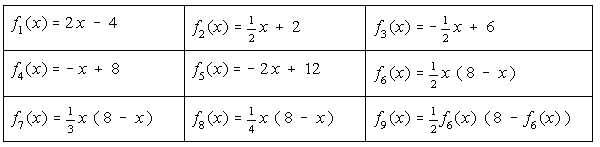
Als Startwert kann jeder Wert genommen werden. In diesen Zeichnungen sollte er zwischen 0
und 8 liegen.
 |
Diese Konvergenzbedingungen ergeben sich beim
Experimentieren. Umgang mit Parabeln und Fixpunktberechnungen sind willkommene Möglichkeiten, wichtige Grundtechniken am Anfang von Klasse 11 einzuüben. Ist der Ableitungsbegriff noch nicht vorhanden, so kann hier eingesehen werden, wie
wichtig es ist, sich über die Steigung von Kurven Klarheit zu verschaffen. |
https://mathe.web.leuphana.de http://mathematik.uni-lueneburg.de |