Fraktale Geometrie Leitseite URL haftendorn.uni-lueneburg.de/mathe-lehramt/fraktale/fraktale.htm

[Fraktale] [Programme]   © Prof. Dr. Dörte Haftendorn

Wegfraktale Lindenmayer-Systeme

Grundlegendes Realisierungen Zweig-Arbeitsblatt Dimension Zweigfraktal LOGO Pascal L-System Texte, Literatur, Links Box-Dimension

Fraktale Leitseite

Wegfraktale mit Turtlegrafik      Wegfraktale mit Lindenmayersystem Lindenmayer-Java-programm auf der schweizer Site http://www.natur-struktur.ch

Galerie der Wegfraktale

Fraktale entstehen sehen! Java-Applets für Wegfraktale und Lindenmayersysteme

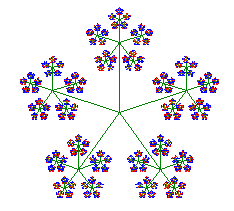Java-Applets: Zusehen, wie die Stufen der Fraktale nacheinander entstehen

Grundprinzip

Initiator ist meist ein gerader Strich, allgemein ein Linienelement.

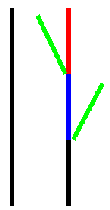
Der Generator ist aufgebaut mit den Linienelementen des Initiators. Der Generator klärt, durch was der Initiator ersetzt werden soll. Am einfachsten geht es, wenn man den Generator aus geraden gleichlangen Stücken zusammensetzt.

Regel:

Jedes Linienelement (zunächst des Generators,dann in jeder Stufe) wird durch den verkleinerten Generator ersetzt. Das wird stets wiederholt.

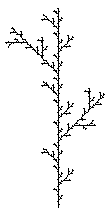
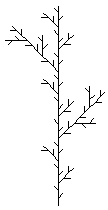
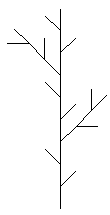
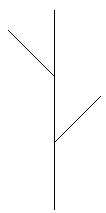
So entsteht stufenweise ein immer vielfältiger verzweigtes Bild. Dabei werden die kleinsten geraden Zweiglein immer kleiner. Bei diesem Zweig ist der Verkleinerungsfaktor 1/3. Dadurch gelangt man recht bald an die Grenzen der Darstellbarkeit. Das mathematische Fraktal ist die Grenzfigur dieses Prozesses. Man kann das Fraktal denken, sehen kann immer nur Vorstufen.
Stets wird beim Zeichnen ein Weg durchlaufen, deshalb habe ich diese Fraktale Wegfraktale genannt. In der einschlägigen Literatur wird meist nur "klassische Fraktale" (weil es sie schon länger gibt) gesagt, oder sie bekommen den Namen L-Systeme, nach Lindenmayer. Auch den Namen Graphtale habe ich schon gelesen.
Es sind vielfältige Variationen dieses Prinzips möglich, z.B. können zwei Generatoren im Wechsel oder in zufälliger Wahl wirken. Es könnten auch nur ein Teil des Linienelementes ersetzt werden u.v.m.
Der Kreativität werden (fast) keine Grenzen gesetzt.

Realisierung von Hand: Zumindest bei einigen im Karopapier realisierbaren Generatoren kann man drei bis vier Schritte ganz brauchbar zeichnen. Sicher sind solche Fraktale der erste Schritt im Unterricht.

Realisierung mit rekursiven Prozeduren, z.B. in LOGO

PR zweig :n :a

lokal "x"  lokal "y"    vi

     wenn :n=0 dann  vw :a rückkehr

     zweig :n-1 :a /3   re :wi

     setze "x"  xko  setze "y" yko

     zweig :n-1 :a /3    sprung :x :y   li :wi

     zweig :n-1 :a /3        li :wi

     setze "x"  xko  setze "y" yko

     zweig :n-1 :a /3    sprung :x :y    re :wi

     zweig :n-1 :a /3

ENDE

vw :a weist den "Igel" an, a Pixel vorwärts zu laufen. re :wi und li :wi sind Drehungen der Blickrichtung um die Gradzahl :wi. Im Befehl setze werden die momentanen Koordinaten gemerkt und bei sprung wieder angesprungen. Damit werden die Verzweigungsknoten realisiert. In der Arbeit mit LOGO habe ich einige Erfahrung. In diesem Thema ist LOGO außerordentlich geeignet.

Realisierung mit rekursiven Turtlegraphik-Prozeduren in Pascal
Eigentlich gibt es keine Turtlegraphik mehr in Pascal. Gerade wegen dieses Themas habe ich aber eine turtle-Unit geschrieben, die die mit der alten (Version kleiner 4) Pascalsyntax, die an das engliche LOGO angelehnt war, wieder verfügbar macht. Sie können diese und dasProgramm zweig.pas und zweig.exe © Ha94herunterladen.

Beachten Sie unbedingt die Hinweise zum Laden meiner Pascalprogramme. Mit dem Programm zweig kann man etwa 20 Fraktale in jeder sinnvollen Stufe zeichnen.

Realisierung mit Lindenmayer-Systemen Ursprünglich wurden die L-Systeme 1968 von dem Biologen Aristid Lindenmayer zur Beschreibung des Pflanzenwachstums entwickelt.
Aus einem Axiom und einer oder mehreren Ersetzungsregeln wird zuerst entsprechend der gewählten Stufe ein langes Wort gebildet. Dessen Buchstaben werden dann einzeln gelesen und in Turtlegraphik-Befehle umgesetzt. Dabei steht F z.B: für fd(a), + für lt(b) , - für rt(b) bei einer Realsierung in Pascal, b.z.w. F z.B: für vw :a, + für li :b, - für re :b bei einer Realsierung in deutschem LOGO. In englischem LOGO steht fd statt vw, lt statt li und rt statt re. Die Klammern markieren die "Knoten", an denen die Zweige beginnen.

Mit diesem Prinzip sind auch die obigen JAVA-Applets erzeugt. Weiteres in der Galerie der Wegfraktale.

Zweig-Fraktal

1. Das Axiom F (Stufe 0).
2. Die Ersetzungregel für F ist F ( + F ) - F ( - F ) + F (Stufe 1).
3. In Stufe 2 ist dann F ( + F ) - F ( - F ) + F ( + F ( + F ) - F ( - F ) + F ) - F ( + F ) - F ( - F ) + F ( - F ( + F ) - F ( - F ) + F ) + F ( + F ) - F ( - F ) + F entstanden.
4. Für Stufe 3 ist wieder jedes F mit der Ersetzungsregel zu ersetzen, u.s.w. .
5. Wegfraktale mit Lindenmayersystem

Die Länge der Lindenmayerworte wächst immens schnell, hier etwa exponentiell mit Basis 5. Das bringt progammiertechnische Probleme, die ich aber in dem Programm linde.pas bzw. linde.exe © Ha94 gelöst habe.

Beachten Sie unbedingt die Hinweise zum Laden meiner Pascalprogramme. Mit dem Programm linde kann man ohne Programmierkenntnisse Fraktale in jeder sinnvollen Stufe zeichnen, kreativ Regeln variieren oder erfinden und schöne Kreationen speichern und laden.

[Fraktale (Leitseite)] [Wegfraktale] [Programme]

Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn (1996)(2002) Apr. 2005, update 18. April 2012

Direkte Internetadressen [www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]