Box-Dimension D

Box-Dimension	Messung der Boxdimension	Raster für Boxdimension
Diese Seite besser als	Messung der Boxdimension allgemein	Messungs-Beispiel für 2 Raster

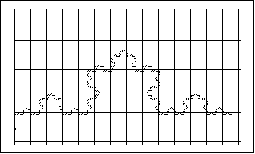
Kästchenlänge oben =	Fraktal derselben Stufe wie im mittleren Bild. Gezeichnet mit weitem Raster. Es werden m _weit Kästchen getroffen. Die Kästchen sollen eigentlich quadratisch sein, Evt. zeigt die Abbildung das nicht deutlich. Entsprechende Bilder mit Rasterung können extra angesehen werden.
Kästchenlänge der Mitte • 3	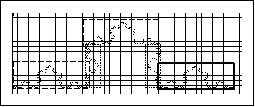Ausgangsbild,enges Raster Es werden *m_eng* Kästchen getroffen. Überlegung: In dem dicken Rahmen werden genau so viele Kästchen getroffen, wie im untersten Bild, denn das ist eine wirkliche Ausschnittvergrößerung. Die Anzahl sei m _bau. Die dünnen Kästen zeigen, daß sicher gilt: *m_eng* > (3 + Wurzel(3) ) m _bau. > 3 m _bau
Baustein aus der Mitte • 3 = unten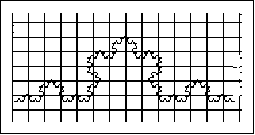	Dies ist eine wirkliche Ausschnittvergrößerung des dick eingerahmten Bausteins. Die Kochkurve darin ist daher nicht so fein untergliedert wie das Fraktal in der Mitte. (Die Stufe ist um 1 geringer.) Bei einem wahren (idealen) Fraktal ist aber so eine Ausschnittvergrößerung wieder genauso wie das wahre Fraktal.

Dem Eindruck der wahren Fraktals kommt die oberste Zeichnung näher. Obwohl dort das Fraktal feiner gezeichnet ist, gilt etwa m_bau int ungefähr m _weit.
Zusammen gilt sicher deutlich: m_eng > 3 m _weit > k m _bweit Also ist die Kochkurve keine normale Linie. Für das wahre Fraktal ist dann die Gleichung 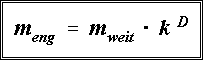sinnvoll, und der Exponent D heißt Boxdimension des Fraktals.
Dabei ist k der Streckfaktor von der engen Kästchenlänge auf die weite Kästchenlänge.
m_eng bzw. m_weit ist die Zahl der Kästchen, die bei engem, bzw. bei weitem Raster von dem Fraktal getroffen werden.
So ergibt sich die Möglichkeit, aus zwei Zählungen die Boxdimension näherungsweise zu bestimmen.
Man kann auch mehr als zwei Zählungen desselben Fraktals auswerten, das ist extra erläutert.

Bei der Kochkurve und anderen überschneidungsfreien Fraktalen stimmt die Boxdimension D mit der Selbstähnlichkeitsdimension d überein. Das kann man sich plausibel machen. Beweise gehen auf die Hausdorff -Dimension zurück. Im Überschneidungsfall ist D < d. Damit ist die Boxdimension eher als die Selbstähnlichkeitsdimension geeignet das äußere Erscheinungsbild der fraktalen Figur zu beschreiben. Bei 1 < D < 2 ist das Fraktal um so linienähnlicher je dichter D an 1 liegt, und um so flächiger, je dichter D an 2 ist. Mit räumlichen Gittern kann man auch Boxdimensionen von fraktalen Körpern (Schwämmen, Riffen, Wolken, Baumkronen, Lungen,..) bestimmen.

[Fraktale] [Wegfraktale] [IFS-Fraktale] [Dimension] [Programme]

(1996)(2002) Apr. 2005, update 14. August 2011

Direkte Internetadressen
[www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt]

Fraktale Dimension	Hinführung zum Begriff	Selbstähnlichkeits-Dimension
Box-Dimension	Messung der Boxdimension	Raster für Boxdimension