www.mathematik-verstehen.de	https://mathe.web.leuphana.de	© Prof. Dr. Dörte Haftendorn
https://mathe.web.leuphana.de/fraktale/fraktale.htm [Fraktale Leitseite] [Rekursion] [Weg-Fraktale] [Dimension] [IFS] [Mandel...] [Natur] [Dynamik] [Automaten] [Programme download]

Messung der Boxdimension

Boxdimension	Messung der Boxdimension	Raster für Boxdimension
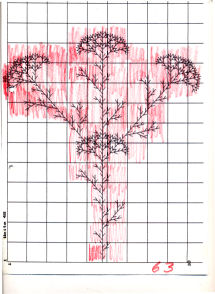
Boxdimension	Diese Seite besser als	Messungs-Beispiel für 2 Raster

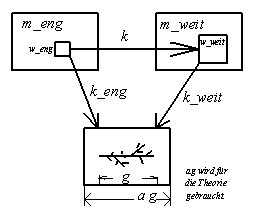Es gilt die Gesetzmäßigkeit 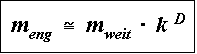. Dabei ist w die Gitterweite und m die Zahl der Kästchen, die vom Fraktal getroffen werden. Die Seite Boxdimension begründet diese Formel.
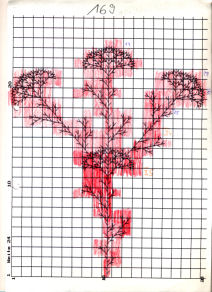
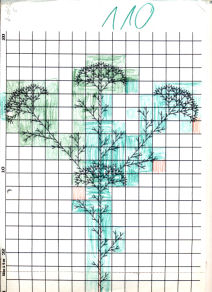
Hat man mehr als zwei Messungen, so ist es sinnvoll, sie gemeinsam graphisch auszuwerten. Dazu braucht man eine Bezugsgröße g, interpretierbar als Pixelbreite des Fraktals.

Aus dem Bild rechts ist (mit Operatoren) direkt ablesbar: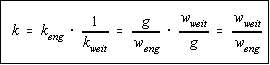

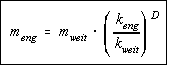also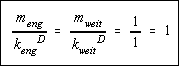

Die beiden Einsen in dem Bruch beziehen sich darauf, daß man als weites Raster auch den unteren Kasten nehmen kann. Ein Kasten, der von dem Fraktal getroffen wird, Streckfaktor 1 auf sich selbst.

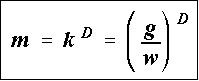Damit ist die Kennzeichnung von eng und weit unnötig geworden. Der Streckfaktor von der Rasterweite auf die ganze Weite g sei nun k _ganz . Dann gilt: . Dies ist in doppelt-logarithmischer Auftragung eine Ursprungsgerade. Die Gleichung ist aber streng genommen nur richtig für m bei dem wahren Fraktal. Es zeigt sich auch, daß wirklich erzeugte Messpunkte zwar mit erfreulicher Genauigkeit in doppelt-logarithmischer Darstellung auf einer Geraden liegen, jedoch nicht auf einer Ursprungsgeraden. Dieses Verhalten kann man erklären und merkt dabei, daß die Steigung dieser Geraden aber weiterhin D ist
Durchführung der Messung:
Gerasterte Fraktalbilder ist hier verfügbar oder mit meinen Programmen Linde und Zweig herstellbar.

Auszählungen zur Bestimmung der Boxdimension von Fraktalen
Diese Anleitung als pdf-Seite

k= Größe des Fraktals in Karos, links ablesbar, beim 1. Bild ist k=47
Die auf den Bildern angegebene Weite w sind Pixel-Anzahlen. Alle Bilder sind 630 Pixel lang, also also sind sie g=630/w = Karos lang.damit kann man k auch ausrechnen, wie es weiter unten gemacht wird. Auszählen ist didaktisch aber besser.
m= Zahl der vom Fraktal getroffenen Karos. (Wurde von Schülern gezählt).
Trage die Punkte (k/m) in doppelt-logarithmischer Darstellung auf, d.h. tragen die Punkte (lg(k) / lg(m) ) in ein gewöhliches Koordinatendsystem ein, und bestimme die Ausgleichsgerade (in Excel=Trendlinie). Ihre Steigung ist die Boxdimension D des Fraktals. Beachte unten die Bemerkung zu "Grenzen" des Verahrens.

	w=12 k= m= lg(k)= lg(m)=		w=24 k= m= lg(k)= lg(m)=
	w=32 k= m= lg(k)= lg(m)=		w=48 k= m= lg(k)= lg(m)=

Boxdimension Berechung une Darstellung

Nochmals die Aufgabenstellung

Zähle auf dem Blatt mit dem gerasterten Fraktal sorgfältig, wie viele Kästchen von dem Fraktal "betreten" werden.
Bestimme eine Bezugsgröße g . Eins der Raster mit Weite W sei K Kästchen breit. Dann ist g=K W.
Lege eine Tabelle an:

1	2	3	4	5
Weite	g/Weite	Log(g/Weite)	m	Log m
36	630/36=17,5	1,243	96	1,9822
...	...	...	...	...

Weiterführen für alle Messungen an diesem Fraktal

Trage die Wertepaare aus den Spalten 3 und 5 in einem Koordinatensystem ein.

Lege mit Augenmaß eine Ausgleichsgerade durch die Punkte. Bestimme ihre Steigung durch Einzeichnung eines Steigungsdreiecks.

Die Steigung ist der gesuchte Meßwert für die Boxdimension D des Fraktals.

Grenzen des Verfahrens: Die Gitterweite muß deutlich kleiner als das Fraktal, aber größer als die kleinste Schrittweite des Fraktals bei dieser Stufe sein.
Gezeichnet ist nie das wahre Fraktal, sondern eine Stufe. Diese muß schon wesentliche Merkmale des wahren Fraktals aufweisen.
Die zufällige Lage des Fraktals im Raster erzeugt Schwankungen der Messpunkte.

Fraktale Dimension	Hinführung zum Begriff	Selbstähnlichkeits-Dimension
Box-Dimension	Messung der Boxdimension	Raster für Boxdimension

[Fraktale] [Wegfraktale] [IFS-Fraktale] [Dimension] [Programme]

(1996)(2002) Apr. 2005, update 05. Januar 2008

Direkte Internetadressen
[www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt]