Fraktale Geometrie Leitseite URL haftendorn.uni-lueneburg.de/mathe-lehramt/fraktale/fraktale.htm

[Fraktale] [Wegfraktale] [IFS-Fraktale] [Dimension] [Programme]   © Prof. Dr. Dörte Haftendorn

Hinführung zum Dimensionsbegriff
Grundüberlegung am Nikolaushaus

Diese Seite als

Zweig-Arbeitsblatt

Das ist das Haus vom Nikolaus.
Es hat eine Weglänge von etwa 17 cm,
einen Flächeninhalt von 5 cm².

Das sind drei Häuser vom Nikolaus.
Sie sind untereinander kongruent.
Sie haben eine Weglänge von etwa 3 mal 17 cm, also 51 cm,
und einen Flächeninhalt von 35 cm².

Das sind z = 9 Häuser vom Nikolaus.
Sie sind untereinander kongruent.
Sie haben eine Weglänge von etwa z17 cm, also 153 cm,
und einen Flächeninhalt von z 5 cm², also 45 cm².

z Häuser haben z-fache Länge
z-fache Fläche
z-faches Volumen

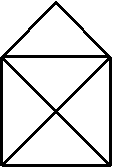Das ist das dreifach so breite Haus vom Nikolaus. Es ist den kleinen Häusern ähnlich, Streckfaktor k=3.
Es hat eine Weglänge von etwa k 17 cm, also 51 cm,
eine Breite von k2 cm, also 6 cm
und einen Flächeninhalt von k² 5 cm², also 45 cm².

Auf das k-fache gestreckte Häuser haben

• k-fache Länge
• k²-fache Fläche
• k³-faches Volumen

Das Zweigfraktal besteht aus z=5 kleinen Zweigen.

Jeder hat das Maß M_klein.

• Das ganze Zweigfraktal hat daher das Maß 5 M_klein.
• Das Zweigfraktal entsteht aus einem kleinen Zweig durch Streckung mit dem Faktor k=3.
• Das ganze Zweigfraktal hat daher das Maß
  • 3 M_klein , wenn das Maß eine Länge ist.
  • 3² M_klein , wenn das Maß eine Fläche ist.
  • 3³ M_klein , wenn das Maß ein Volumen ist.

Keine der Gleichungen 5=3, 5=3², 5=3³ ist richtig,

Daher ist das für Fraktale sinnvolle Maß weder Länge, noch Fläche, noch Volumen.

Erfüllbar und sinnvoll ist höchstens die Gleichung     z = k ^d

umgeformt: .
Man nennt   d  fraktale Dimension eines selbstähnlichen Fraktals.

Fraktale Dimension	Hinführung zum Begriff	Selbstähnlichkeits-Dimension
Box-Dimension	Messung der Boxdimension	Raster für Boxdimension

[Fraktale] [Wegfraktale] [IFS-Fraktale] [Dimension] [Programme]

Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn (1996)(2002) Apr. 2005, update 24. April 2005

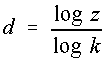Direkte Internetadressen [www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]