Fraktale Geometrie Leitseite URL
haftendorn.uni-lueneburg.de/mathe-lehramt/fraktale/fraktale.htm
[Fraktale] [Programme]   © Prof. Dr. Dörte Haftendorn

IFS-Fraktale

VorbemerkungenIterated Function System = Systeme von Funktionen die "iteriert" werden, d.h. immer wieder ausgeführt werden.
Die fraglichen Funktionen sind meist affine Abbildungen der Ebene in sich. Man kann aber auch übliche Funktionen im x-y-Koordinatensystem nehmen, wie der Cantorsche Staub zeigt. Affine Abbildungen im Raum hat man zum Beispiel beim Mengerschwamm, den ich in meinem Buch auf Seite 94 beschieben habe.
Diese Seiten hier enthalten bieten Erklärungen auf verschiedenen Niveaus, die Anfänge ab 1988 sind seit 1996 im Internet und immer wieder ergänzt worden bis zur Verbindung mit linearer Algebra und den komplexen Zahlen für eine Vorlesung für Lehramtsstudierende.
Besondere Möglichkeiten eröffnen sich durch die Software Cinderella, mit der man ganz frei Fraktale (bis 2D) erfinden und erkunden kann. Hier sind einige Applets und *cdy-Dateien von mir verfügbar. Die Autoren von Cinderella, Prof. Dr. Jürgen Richter-Gebert und Prof. Dr. Ulrich Kortenkamp, pflegen selbst an der TU München eine reichhaltige Site  Mathe Vital auf der sie unter Punkt 6 bei "Indras Pearls" auch IFS ausführlich behandeln.
Übersicht
Einstimmung in Ordnung und Chaos (Applet)
am Sierpinski-Dreieck
Statische Version mit Text 		Einführung in IFS
Cantorscher Staub
Nach Dufner, siehe Literatur		 Affine Abbildung
einfach erkärt		 Affine Abbildung
mit Linearer Algebra
und Komplexen Zahlen
IFS am Siepinskidreieck IFS erkärt am Waldsee IFS erklärt am Zapfen Pagode
Fraktaler Regen, Chaosspiel Hutchinson-Operator Arnolds Katze Fraktale Dimension
Affine Abbildungen
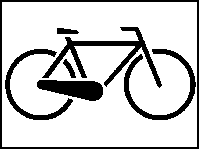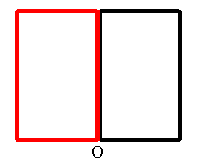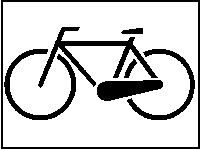einfach erklärt		 Rad,UrbildSpiegelung    
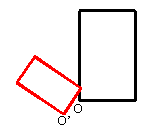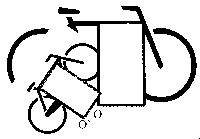Urbild sei das nach rechts fahrende Fahrrad. Ihm entspricht das rechts stehende schwarze Rechteck. Durch das links stehene rote Rechteck ist eine Spiegelung definiert. deren Wirkung ist das nach links fahrende Fahrrad. Das kleine, rote, gekippte Rechteck definiert eine Verkleinerung mit Drehung und Verschiebung.

Die beiden Seiten des Urbildrechtecks könnten auch in ungleichem Maß verkleinert werden und um verschiedene Winkel gedreht werden. Jedes Parallelogramm kann als Bild des Urbildrechtecks aufgefasst werden und definiert dadurch eine sogenannte affine Abbildung. Alle in der Schulgeometrie bekannten Abbildungen sind Sonderfälle affiner Abbildungen:
Kongruenzabbildungen

    affine Abbildungen

    • Ähnlichkeitsabbildungen
      • Kongruenzabbildungen = Deckabbildungen Das Bild eines Rechtecks ist ein Rechteck mit denselben Seitenlängen.
        • Spiegelung
        • Drehung
        • Verschiebung
        • Gleitspiegelung
      • zentrische Streckung, das Bild eines Rechtecks ist ein Rechteck mit demselben Seitenverhältnis.
    • Scherung
    • Achsenstreckung, das Bild eines Rechtecks ist ein Rechteck mit einem anderen Seitenverhältnis.
    • allgemeine Affine Abbildung, das Bild eines Rechtecks ist ein beliebiges Parallelogramm
Affine Abbildungen
mit Linearer Algebra
und auch
komplexen Zahlen
  • Definition Affine Abbildungen sind definiert als parallelentreue und teiverhältnistreue Abbildungen einer Ebene (allgemeiner eines Vektorraumes) in sich.
    Die heißen auch lineare Transformetionen, da ein Punkt p auf einen Punkt p' mit einer Matrix T und einen Translationsvektor t durch die
    lineare Gleichung p' = T p + t abgebildet wird.
  • Die Angabe von drei Paaren aus Urbildpunkt und Bildpunkt definiert eine affine Abbildung. In Cinderella werden affine Abbildungen durch das Anklicken solche Paare direkt definiert.
    Ausfühliche Erklärungsseiten dazu Dabei ist auch der Spezialfall der gleichsinnigen Ähnlichkeitsabbildung, die Drehstauchung mit Translation behandelt, den man schon durch Angabe zweier Punktpaare definiert. Diesen Fall kann man auch statt mit Vektorrechnung auf einfache Weise mit komplexen Zahlen behandeln. Auch das ist auf den genanntenseiten Erklärt.
    Zwei Drehstauchungen mit Verschiebung
    Zwei Drehstauchungen mit Verschiebung mit Abbildungsgruppe
    Zwei Drehstauchungen mit Verschiebung mit Abbildungsgruppemit IFS-Fraktal
  • Iterierte Ähnlichkeitsabbildung bei Mathe-Vital (Prof. Richter-Gebert TUM München)
    Dasselbe als IFS   
    • Sierpinkski-Dreieck
  • Ordnung und Chaos als Überraschung erfahren (Applet)
  • Sierpinskidreieck (statisch) Text zum Applet, das sich sehr bewährt als allererster Eindruck und Sensibilisierung für den Zusammenhang von Chaos und Ordnung. Dazu mein altes Pascalprogramm sierpi.exe starten, siehe Programme
  • Sierpinski-Dreieck als IFS-Fraktal
    • IFS Waldsee

    "Waldsee-Fraktal"

    Dieses IFS-Fraktal entsteht dadurch, dass zwei Abbildungen definiert werden und dann ein beliebiger Startpunkt mit diesen Abbildungen sehr oft abgebildet wird. Für das Wald-Fraktal wird das blaue, gestrichelte Rechteck auf das rote links oder auf das grüne rechts abgebildet. Die rote Abbildung bewirkt Verkleinerung und die Drehung nach links, das grüne Verkleinerung und das Verrücken nach rechts.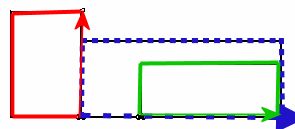

    Gute Seite zum Waldsee-Fraktal
  • Waldinsel interaktiv
    Waldinsel interaktiv mit Hutchinson-Operator

    • Der "Wald" ist die Grenzfigur, der Limes, der Attraktor dieses Abbildungsduos. IFS ist die Abkürzung für "iterated functions". Die Form der Grenzfigur hängt allein von den Abbildungen ab, die man in dem von mir entwickelten Computerprogramm kreativ und frei wählen kann.
    IFS Zapfen
  • Dies ist mein Zapfen, ein Verwandter des Barnsleyfarnes.

    Abbildungen Zapfen


    Man sieht das schwarze Startrechteck.
    Die blaue Abbildung sorgt für die Spiegelung und damit die Symmetrie des Zapfens.
    Die grüne Abbildung ist für den "Körper" zuständig. Sie hat die schwächste Kontraktion.
    Die rechte rote Abbildung erzeugt die Zweige und ist vor allem für die Struktur des Zapfens verantwortlich.
    Die kleine lilafarbene Abbildung und der schwarze Strich sorgen für den Stiel.

    Der Zapfen entsteht nun durch den "fraktalen Regen",
    Zapfen mit Abbildungsgruppemit IFS-Fraktal

    • Fraktaler Regen
    Chaosspiel
    Die IFS-FRaktale entstehen nach der Definition der Abbildungen durch den "fraktalen Regen", Peitgen nennt es das "Chaosspiel":
    Der Ursprung ist Startpunkt.
    1. Eine der Abbildungen wird zufällig ausgewählt.
    2. Der Punkt wird mit der Abbildung abgebildet und in der Farbe der gewählten Abbildung gezeichnet.
    3. Es geht bei 1. wieder los.
    Dies alles kann man bei den Cinderella-Applets und *.cdy-Dateien besonders gut verfolgen.
    Weiter ausführliche Erläuterung für Schüler, die 1999 eine Facharbeit schreiben wollten, finden Sie auf einer nahExtra-Seite

    Nach etwa 100000 Wiederholungen ist das Bild in Bildschirmgröße fertig. Sieht man von der Pixelrealisation ab, ist das Bild das Limesbild, das Grenzbild, der Attraktor dieses Abbildungssystems, daher der Name "Iteriertes Funktionen-System" und IFS-Fraktal.

    [Fraktale (Leitseite)] [IFS-Fraktale] [Programme]
    Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn (1996)(2002) Apr. 2005, update 14. August 2011
    Direkte Internetadressen
    [www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]