Fraktale Geometrie Leitseite URL haftendorn.uni-lueneburg.de/mathe-lehramt/fraktale/fraktale.htm

[Fraktale] [IFS-Fraktale] [Programme]   © Prof. Dr. Dörte Haftendorn

Das Siepinskidreieck
Das Chaos birgt Ordnung

Progamm sierpi.exe bzw. sierpi.pas in ifs.zip. Beachten Sie unbedingt die Hinweise zum Laden

Unter dem Namen "Chaosspiel" ist das Verfahren später in der mathematischen Literatur aufgetaucht, machmal werden mit "Chaosspiel" aber auch alle IFS-Fraktale beschrieben.
Die folgende beschreibe ich "aktivisch", die Anfänge kann man auch von Hand aus Papier machen. Achtung neu: Applet in moderner Version

Drei Punkte bilden ein gleichseitiges Dreieck. Start ist im oberen Punkt. Wähle einen der Punkte zufällig. Zeichne einen Strich in Richtung auf den gewählten Punkt, zeichne aber nur den halben Weg. Wiederhole 1 und 2 beliebig oft. Hier war also Rechts zweimal gewählt, dann Links, Rechts, Oben, Links.
Hier sind schon etliche Striche gezeichnet.
Allmählich wird das ganze Dreieck schwarz zugemalt. Jeder ist überzeugt: das ist ein chaotisches Strichgewirr.
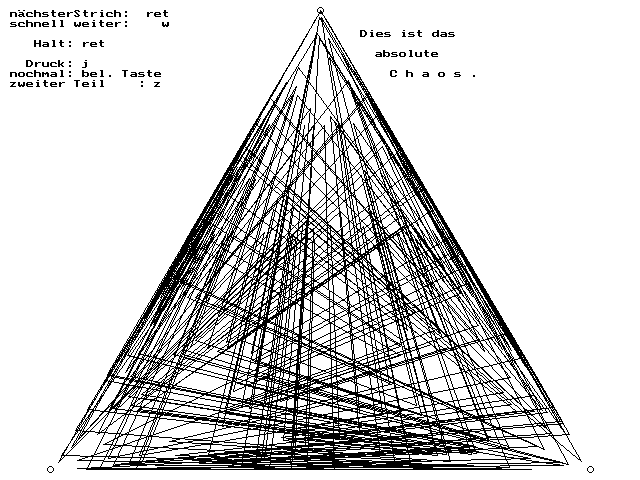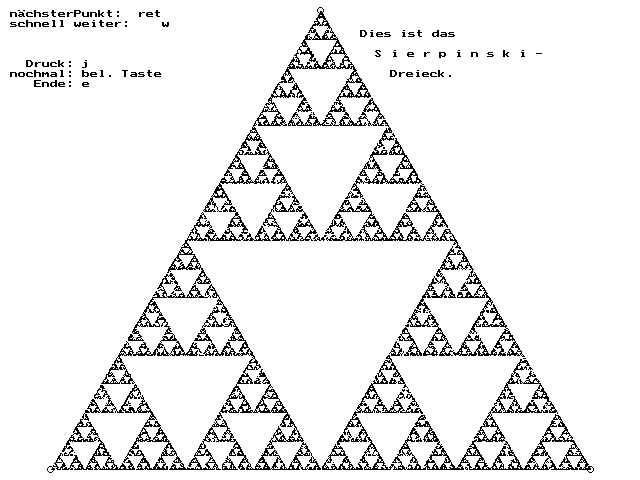
Neuer Start. Winzige Änderung bei Schritt 2: Statt des Striches wird nur sein Endpunkt gezeichnet. Die Punkte sind zunächst schwer zu sehen, werden dann aber mehr und mehr und dadurch deutlich. Im Progamm steht als einzige Änderung statt lineto nun putpixel.
Wenn es nun immer mehr Punkte werden, taucht verblüffenderweise ein wunderbar geordnetes Muster in dem Dreieck auf. Es ist das Sierpinskidreieck, heute eines der bekanntesten Fraktale. Geschichte Das Sierpinskidreieck als Wegfraktal Das Sierpinskidreieck Lindenmayersystem in meinem Programm linde.exe Das Sierpinskidreieck als IFS-Fraktal in meinem Programm ifs.exe

Geschichte des Sierpinskidreieecks

Der Mathematiker und Hochschullehrer Sierpinski hat es 1910 zu dem Zweck in die mathematische Welt gesetzt, dass seine Studenten begreifen, dass sie Begriffe Linie und Fläche durchaus nicht trivial sind.
"Trivial" ist ein Lieblingswort der Mathematiker, was etwa "völlig einfach und offensichtlich" bedeuten soll.
Wenn man nämlich aus einem Dreieck die Mitte herausnimmt und aus den drei Restdreiecken wieder die Mitte, und wieder und wieder...., ist es dann eigentlich noch eine Fläche?
Es ist werder eine Fläche noch eine Linie, es weder Dimension 2 noch Dimension 1, es hat nämlich die Bruchzahl ln(3)/ln(2)=1,58...
es ist ein Fraktal. (fractum, lat.= gebrochen)

Sierpinski-Dreieck als IFS-Fraktal

Pagode

[Fraktale (Leitseite)] [IFS-Fraktale]  [Programme]

Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn (1996)(2002) Apr. 2005, update 16. August 2011

Direkte Internetadressen [www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]