Dreistern-Fraktal

Dies ist ein Dreistern, an dessen Armen Dreisterne sind, die an ihren Armen Dreisterne tragen und so weiter. Sie sehen also ein Dreistern-Fraktal entstehen. Das eigentliche Fraktal muß man sich in Fortführung des Konstruktionsprinzips denken.

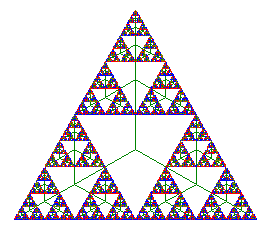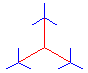
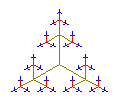
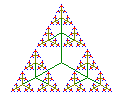
Oben sind die 1., 3. und 5. Stufe zu sehen. Spätestens bei der nebenstehenden 10. Stufe erkennt man, dass das "wahre Fraktal", die Grenzfigur, das

Sierpinskidreieck ist. Die grünen Strich muss man sich dabei fort denken.

Realisierung in LOGO

PR terni :n :a
lokal "x" lokal "y"
wenn :n=0 dann farbe 0 0  255 ternidann :a rk
   setze "x" xko setze "y" yko
      farbe 255/:n 150-150/:n  0
   vw :a terni :n-1 :a/2  punkt :x :y re 120
      farbe 255/:n 150-150/:n  0
   vw :a  terni :n-1 :a/2  punkt :x :y re 120
     farbe 255/:n 150-150/:n  0
  vw :a  terni :n-1 :a/2  punkt :x :y re 120
ENDE

Die Farben sind im RGB-System angegeben.
Erklärung auf den Seiten Farben und Computer.

Diese Prozedur ternidann sorgt für den eigentlichen Dreistern. Im nebenstehenden Fraktal-Hauptprogramm wird dreimal das Fraktal von verkleinerter Stufe mit verkürzten Längen aufgerufen.

PR ternidann :a
lokal "x" lokal "y"
setze "x" xko setze "y" yko
vw :a punkt :x :y re 120
vw :a punkt :x :y re 120
vw :a punkt :x :y re 120
ENDE

Dimension

Das Dreistern-Fraktal ist selbstähnlich. Dabei vernachlässigt man eigentlich die inneren grünen Striche. Es ist zudem überschneidungsfrei, daher lässt sich die Selbstähnlichkeitsdimension ausrechnen:
d=log z / log k , also d = log 3 / log 2 = 1,58.

Selbstähnlichkeitsdimension

Galerie der Wegfraktale

Leitseite Wegfraktale

[Fraktale (Leitseite)] [Wegfraktale] [Galerie] [Programme]

(1996)(2002) Apr. 2005, update 16. August 2011

Direkte Internetadressen
[www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt]