https://mathe.web.leuphana.de/fraktale/rekursion/rekursion.htm[Graphen] [Rekursion] [Weg-Fraktale] [Dimension] [IFS] [Mandel...] [Natur] [Dynamik] [Automaten] [Programme]
 |
Warum gibt es die Bifurkationskaskade?
|
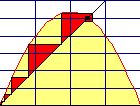
Diese Parabel vom einführenden Arbeitsblatt entspricht der logistischen Parabel für r = 4 , bei der es gar keine stabilen Zyklen mehr gibt. Es gibt übrigens stets periodische Zyklen für exakt rationale Startwerte. Die entziehen sich aber der Ansicht mit dem Computer. Daher sieht man rechts auch gar keine Stabilisierung und es wird (i.w.) der gesamte Wertebereich ausgeschöpft |
 |
|
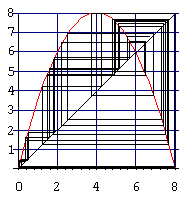
| Diese Funktion ist die zweite Iterierte der obigen Funktion. Mit ihr wird
jeder zweite Wert der obigen Folge berechnet. Wenn es hier einen anziehenden Fixpunkt
gäbe, dann hätte die obige Folge einen stabilen anziehenden Zweierzyklus. Offensichtlich
aber schneidet die Kurve die Winkelhalbierende an allen Fixpunkten steil. In diesem Fall sind auch alle weiteren Iterierten ohne anziehenden Fixpunkt. Also ergibt sich für diese Wahl des Parameters r eine chaotische Bahn. |
 |
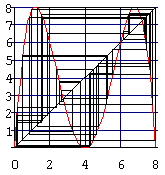| Hier sind die logistische Parabel und ihre zweite und dritte
Iterierte für den Parameter r=3,83 gezeichnet. Man kann sich vorstellen, dass für etwas
kleinere r, z.B. r=3,82 , die drei Extrema der schwarzen Kurve die Winkelhalbierende
gerade noch nicht berühren. Wenn r dann wächst, findet Berührung statt. Das ist dann
der Parameter r, für den das chaotische Verhalten abrupt in einen Dreierzyklus übergeht. Dieser Übergang und die drei Werte sind auf der Feigenbaumseite deutlich zu sehen. Es bleiben bei wachsendem r (im Feigenbaumdiagramm nach unten) solange drei Häufungswerte, bis die 6. Iterierte mit ihren Extrema die Winkelhalbierende berührt. Dann kommt die 12. dran u.s.w., eine Bifurkationskaskade setzt ein. Das geht solange so, bis in der Nähe der Extrema der 3. Iterierten beim Schnitt mit der Winkelhalbierenden der Betrag der Steigung 1 überschritten wird. |
|
|---|---|
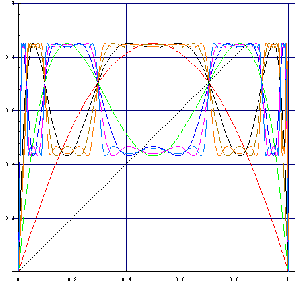
| Hier ist für r = 3,4 die logistische Parabel mit ihren Iterierten bis
zur 8. Iterierten gezeichnet. Die n. Iterierte ist ein Polynom 2n-ten Grades. Die 8. Iterierte ist also ein Polynom 256-sten Grades. Alle gezeichneten Iterierten (und auch alle weiteren) haben genau zwei „flache“ Schnittstellen mit der Winkelhalbierenden. Also gibt es für r=3,4 einen stabilen Zweierzyklus, oder zwei Häufungswerte. Das kann man auch am Feigenbaumdiagramm sehen. Es ist das Gebiet nach der ersten Bifurkation, im ersten „Hügel“ von oben. Für größer werdende r sackt das mittlere Extremum weiter nach unten, wenn dann alle „Schnittsteigungen“ größer 1 werden, wird das Verhalten der Folgen chaotisch. |
 großes Bild 15 K |
|
[Graphen]
[Rekursion]
[Weg-Fraktale]
[Dimension]
[IFS]
[Mandel...]
[Natur]
[Dynamik]
[Automaten]
[Programme]
|
 Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn (1996) Nov. 2002, update |
| www.mathematik-verstehen.de www.doerte-haftendorn.de https://mathe.web.leuphana.de http://mathematik.uni-lueneburg.de |
