| Didaktik |
Aufbau einer Einheit zu Folgen, die die Analysis begründet.
- Als Einstieg eignen sich die rekursiven Folgen. Dieses ist auf der Extraseite Rekursion
 ausführlich dargestellt und didaktisch begründet
- Beispiele zur Beweisbedürftigkeit leiten zu Vollständigen Induktion
- Diese wird durch den "Russischen Zahlmeister" als gedankliches Instrument herasugestellt
- Grenzwerte sind aus dem rekursiven Teil schon bekannt und werden nun bei expliziten Folgen sauber definiert.
- Summenfolgen mit Anregung aus "figurierten Zahlen" regen das selberfinden von Formeln an und bieten nochmals Beispiele für vollständige Induktion
- An dieser Stelle kann die Überleitung zu den unendlichen Reihen erfolgen.
Dazu Extraseite "Reihen ". Der Beginn ist mit geometrischen Folgen und Reihen sinnvoll
- Ab der Mittestufe ist das Thema Wachstum sinnvoll. Auch dies steht auf einer Extraseite Wachstum
- Für die freie Arbeit von Lernenden im Thema Folgen ist GeoGebra bestens geeignet.
Seit der Version 3 können auch Folgen bequem dargestellt werden.
|
| Rekursion |
|
Explizite Folgen
Vollständige Induktion |
|
Explizite Folgen
und Grenzwerte |
|
| Summenfolgen |
|
| Reihen | Eigene Leitseite zu Reihen |
| Wachstumsfolgen |
Im Rahmen dieses Lehrgangs bietet es sich an, die üblichen Wachstumsfolgen sowohl explizit als auch rekursiv zu betrachten.- Linares Wachstum, Trägerfkt. parallel zur Winkelhalbierenden
- exponentielles Wachstum, Trägerfkt. Urspungsgerade
- begrenztes Wachstum, .Gerade mit flacher Steigung, die die Winkelhalbierende schneidet. (wie auf dem Rekusrions-Einführungsblatt)
- logistisches Wachstum Trägerfkt. Parabel mit gewissen Eigenschaften
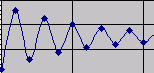  Wachstum und Zerfall, Modellierung in der Mathematik, Eigene Leitseite 
Siehe eigene Leitseite auch zu Rekursion
|
Weitere Folgen
Sek II, Hochschule
Informatik |
Folgen Sek II
Aufwendigere Folgen lassen sich mit "Umdefinieren" mit den Dateien für einfache Folgen untersuchen. Insgesamt gibt es mathematisch sehr anspruchsvolle Folgen -und erst recht Reihen- wo der Computer nur bescheidene Möglichkeiten bietet.
Darunter sind insbesondere die sehr schnell wachsenden Folgen, z.B. Ackermannfolge, die das Problem der Berechenbarkeit aufwerfen.
Interessant sind auch die Folgen mit "unvorhersagbarem" Verhalten wie z.B. die Laugwitzfolge (=Ulamfolge, =Hagelkornfolge)
Ein Riesenfeld eröffnen die komplexen Iterationsfolgen. Diese sind Im Bereich "Fraktale" untersucht.
|
| Werkzeuge |
Werkzeuge, die interaktive Möglichkeiten haben, Erkundungen der Lernenden erlauben:
In reinen Graphenzeichnern können die hier gebenen Anregungen z.T. umgesetzt werden.
 GeoGebra
Seit Aug. 07 kann auch GeoGebra Folgen mit einem komfortablen Befehl erzeugen und zeichnen. |
 Dynageo
Folgenerzeugung nur Einzelpunktweise |
 MuPAD
lässt keine Wünsche offen,
hat auch interaktive Möglichkeiten |
 Excel |
 Derive
Achtung, Auslaufmodell, wecheln Sie zu MuPAD |
Applet, Java,
in jedem Browser |
ActiveX,  nur
Internet-Explorer |
Ansicht in jedem Browser 
 |
nicht im Browser | nicht im Browser |
Download  |
Download  |
Download
 Ziel speichern unter... |
nur als Download  | Derive ist hat gute Schieberegler
aber nicht im Web |
Als weiteres Werkzeug für diesen Bereich istTurboplot geeignet.
Didaktisch wertvoll ist die Umschaltbarkeit zwischen den üblichen Zeit-Graphen und der Spinnwebgraphen.
Dazu ist auch das Attraktor-Diagramm (=Feigenbaum-Diagramm) und die Betrachtung der Iterierten möglich. |
 TI voyage: - Man wählt mode sequence(Folgen)
- dann y=-Fenster
- man traägt z.B. ein: u1(n)=4-1/n^2 für eine expliziete Folge und z.B. u2(n)=3*u2(n-1)*(1-u2(n-1)) mit ui2=0.1 für eine rekursive Folge. Das i in der Buchstabenfolge heißt "initial"=Startwert.
- Bei F7 Axes (Achsen) wählt man time=Zeit für explizite Folgen und web=Netz mit trace=Spurflg für rekursive Folgen.
- Mit Diamant Graph wird im letzteren Fall gleich die Winkelhalbierende und die Trägerfunktion eingezeichnet.
- Mit F3 und der West-Pfeil-Taste erzeugt man die Treppchen
.
|
|
|
Alle mathematischen Computerwerkzeuge sind für Funktionen und Graphen geeignet.
Lesen Sie die Informationen zu
     Interaktiven Seiten |
|
|
Site-Info
Heronverfahren mit Rechtecken, edel
Heronverfahren mit TI Nspire 2011 (NEU !!!! 
TI-nspire-Datei dazu
Lerndatei MuPAD 4 Folgen, Mengen, Listen und ihre Graphen
Folgen-Übung von Hand
MuPAD:
im Calculus-Menu Nr 4
TI-nspire-CAS Datei dazu