www.mathematik-verstehen.de
Link zum Buch
[Folgen] [Rekursion] [Analysis] [Didaktik] [Computer] [Graphen]
www.mathematik-verstehen.de |
| Link zum Buch |
|
https://mathe.web.leuphana.de/analysis/reihen/reihen.htm
[Folgen] [Rekursion] [Analysis] [Didaktik] [Computer] [Graphen] | ||
Reihen | Folgen |
| Reihen aus einfachen Folgen |
|
| Geometrische Reihen | 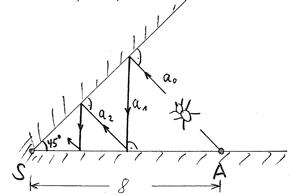 Klausur zu Folgen und Reihen mit der Spinnenaufgabe Klausur zu Folgen und Reihen mit der Spinnenaufgabe |
| Taylorreihen |
Das Beispiel greift die Betrachtung von Arens et al. "Mathematik" S. 317 (einem empfehlenswerten Gesamtwerk) auf. Es zeigt sich, dass die Restgliedbetrachtung gröber ist. Für mich ziehe ich das Fazit: die Mühe mit der Herleitung des Restgliedes lohnt sich in Lehrzusammenhängen außerhalb der höhren Semester eines Mathematikstudiums nicht. Mit passenden Werkzeugen kann man dei Differenz zwischen Funktion und Taylorpolynom sogar genauer direkt untersuchen. Da kann in Schule und Grundstudium wertvolle interaktive Mathematik betrieben werden. |
| Fourierreihen | |
| Riemann | Die besonderen exotischen Reihen, die für Riemann der Anlass waren, die Integralrechnung auszubauen sind auf der Riemann-Mathematik-Leitseite |
www.mathematik-verstehen.de |
[Folgen]
[Rekursion]
[Analysis]
[Didaktik]
[Computer]
[Graphen]
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn |
Link zum Buch |
| www.leuphana.de/matheomnibus www.doerte-haftendorn.de https://mathe.web.leuphana.de http://www.mathematik-sehen-und-verstehen.de |