www.mathematik-verstehen.de
© Prof. Dr. Dörte Haftendorn

Link zum Buch
Site-Info
https://mathe.web.leuphana.de/analysis/analysis.htm
[Analysis]  [Didaktik]  [Computer]  [Funktionen und Graphen]  [Numerik] 

Nullstellen bestimmen

ZusammenhangMit f(x)=0 wird aus einem Nullstellenproblem eine Gleichung.
Andererseits lässt sich jede Gleichung von einer Variablen als Nullstellenproblem formulieren.
Gleichungen Didaktische Vorgehensweise der Sek I und exakte Methoden haben eine eigene Leitseite "Gleichungen"
Dort sind alle Gleichungstypen systematisch behandelt.
NullstellenIn der Analysis werden einige Fragen auf Nullstellenprobleme zurückgeführt. Auf dieser Seite stehen die Methoden im Mittelpunkt, die man üblicherweise dafür braucht.
Die nachfolgenden Skizzen kann man alle noch an der x-Achse spiegeln.
Nullstellen von Geraden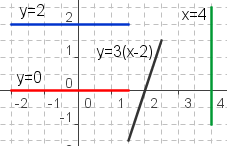
    Lineare Gleichungen
  1. Unendliche viele Nullstellen hat die x-Achse selber, y=0
  2. Keine Nullstelle hat y=b mit b ungleich 0
  3. Genau eine Nullstelle hat jede andere Geraden-Funktion y=m x + b
  4. Genau eine Nullstelle hat auch die senkrechte Gerade x=a
  5. Die Gerade y=m(x-a) hat die Nullstelle a
Nullstellen von Parabeln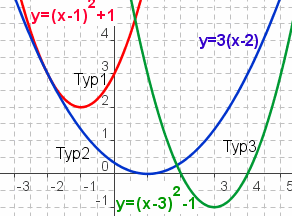
    Quadratische Gleichungen
  1. keine Nullstelle, Parabel zu hoch (oder zu tief)
  2. doppelte Nullstelle, Parabel brührt die x-Achse
  3. zwei Nullstellen, symmetrisch zur Scheitelstelle gelegen.
Existenz von Nullstellen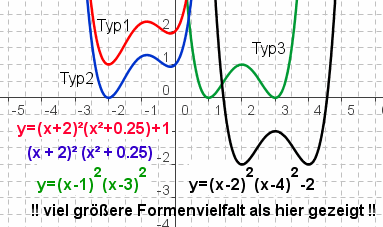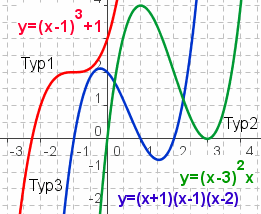
  1. Alle Polynome ungeraden Grades haben mindestens eine Nullstelle,
    denn sie verlaufen stetig von minus unendlich nach plus unendlich.
  2. Wenn dies nicht die einzige Nullstelle ist, dann haben sie mindestens zwei weitere Nullstellen, die evt. zusammenfallen.
  3. Alle Polynome geraden Grades haben eine gerade Anzahl von Nullstellen, wenn man die Vielfachheit berücksichtigt, nämlich 0 oder 2 oder 4 oder 6.... Nullstellen.
  4. Ein Polynom n-ten Grades hat höchstens n Nullstellen. Im Komplexen hat es genau n Nullstellen (mit Vielfachheiten gezählt).
    Mehr zum Fundamentalsatz und Vieta-Wurzelsatz
Nullstellen von Polynomen
  • Handwerkszeug für Polynome:Hornerschema, GRT, CAS
  • Hornerschema Übersichtsblatt    Hornerschema von Hand mit der vollständigen Zerlegung in Linearfaktoren
  • Sonderfall: es existieren ganzzahlige Lösungen:
    Schritt I: Ausklammern soweit möglich
    Schritt II Suche (mit Horner-Schema) ganzzahliger Nullstellen als Teiler des Absolutgliedes
    Schritt III Restpolynom als Hornerschema (s.u.) ablesen (oder Division durch (x-xo))und wiederholen ab Schitt 2 oder Restpolynom=0 als quadratische Gleichung oder mit den oben genannten Methoden lösen.
    Weiteres z.B. zu mehrfachen Nullstellen steht auf der Leitseite Polynome
  • Mehrfache Nullstellen, Vielfachheit einer Nullstelle, Grad einer Nullstelle
  • Exakte Methoden für Polybome 3. und 4. Grades stehen bei Gleichungen
  • Niels Henrik Abel bewies 1824, dass für Polynome ab dem 5. Grad keine allgemeinen Lösungsverfahren existieren können. Diese Polynome sind nur noch in Sonderfällen exakt lösbar.
Iterative Verfahren
Numerische Bestimmung von Nullstellen
besondere Gleichungen
;

© Prof. Dr. Dörte Haftendorn
www.mathematik-verstehen.de
 [Analysis]  [Didaktik]  [Computer]  [Funktionen und Graphen]  [Numerik] 
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Nov. 2002, update 14. Juli 2013 		Site-Info
Link zum Buch
www.leuphana.de/matheomnibus       www.doerte-haftendorn.de
https://mathe.web.leuphana.de     http://www.mathematik-sehen-und-verstehen.de