www.mathematik-verstehen.de
© Prof. Dr. Dörte Haftendorn

Link zum Buch
Site-Info
URL
haftendorn.uni-lueneburg.de/mathe-lehramt/analysis/polynome/polynome.htm
[Analysis]  [Funktionen und Graphen]  [Parabeln]  [Polynome im Affenkasten] [Nullstellen] [Computer] [Numerik] 

Polynome

Diese schöne und wichtige Funktionenklasse bekommt nun hiermit eine eigene Leitseite
Damit sollen alle Elemente zusammengeführt werden, die auf dieser Website vielleicht zu verstreut sind.
Geraden ...Die Seite Nullstellen enthät eine sytematische Übersicht zu diesem Problemfeld
Parabeln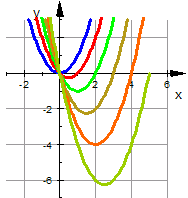Auch sie haben eine eigene Leitseite bekommen, denn sie bilden in der Schule das Tor zum Verständis von Funktionen überhaupt.
Daher kommen sie bisher mehr integriert in die anderen Themen vor. Aus Sicht von Lehrenden und Lernenden, die sich vorläufig allein den Parabeln widmen wollen, sind auf der Leitseite die Sachen zusammengestellt, die sich auf dieser Website auf Parabeln beziehen.
Vietascher Wurzelsatz für Parabeln
Definition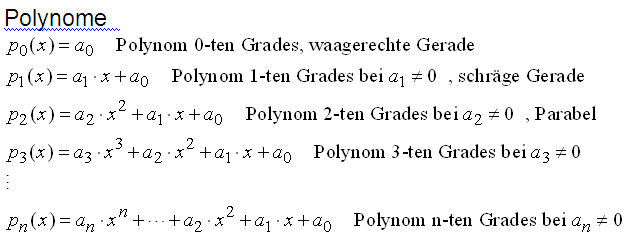
  • Polynom 4. Grades mit frei variierbaren Koeffizienten
    		•
    Polynome, die vorgegebene Punkte treffen Ein Polynom n-Grades kann durch n+1 Stützpunkte exakt gelegt werden, wenn keine zwei dieser Punkte dieselbe Stützstelle aber unterschiedliche Stützwerte haben. (Klar, das widerspäche dem Funktionsbegriff.)
    Ein solches Polynom heißt "Interpolations-Polynom" Für seine Beschaffung existieren zwei gute Konzepte: Newtons Interpolationspolynom und das Lagrange-Interpolationspolynom. Sie beide finden aber bei denselben Punkten auch dasselbe Polynom. Das Thema Interpolation gehört eigentlich in die Numerik. Aber die Früchte können wir hier ernten und gut gebrauchen.
  • Polynom durch 6 frei ziehbare Punkte
    Diese Datei ist nach dem Konzept von Newton aufgebaut. Daher ist es möglich, sie auch für Polynome durch weniger Punkte zu gebrauchen. Man muss dann nur n(x) deaktivieren und ein passendes der hi anzeigen.
    Man kann also ohne F h4 nehmen, ohne F und ohne E gilt h3 u.s.w..
    Anleitung für Definition dieser Funktionen   [mehr zum Konzept]
  • Polynom durch 4 frei ziehbare Punkte
    Diese Datei ist nach dem Konzept von Lagrange aufgebaut. Sie erfordert bei der Definition schon auf eine feste Zahl von Punkten. Dafür ist das Konzept leichter erklärbar.    [mehr zum Konzept]
  • Vietascher Wurzelsatz für den Zusammenhang zwischen Nullstellen und Koeffizienten
  • Mehrfache Nullstellen nach Vieta
    • Der EdelsteinPolynome in Affenkasten

    Polynome im Affenkasten

    sind mein "Urgestein".
    Es handelt sich um wunderbare Möglichkeiten für Erkundungen und entdeckendes Lernen in jeder Lerngruppe, die Polynome im Lehrplan hat.
    Leitseite 2. Grad 3. Grad 4. Grad Potenzfkt. Euler-Kasten
    Kurvendiskussion
  • Weiteres zu Polynomen und Kurvendiskussionen
  • Interaktive Erzeugung alle möglichen Typen von Polynomen 4. Grades
  • Vollständige Übersicht über alle Polynpme 4. Grades (sprechende Graphen)   und dazu auch die Funktionsterme
    alle Polynpme 4. Grades       
    • Potenzfunktionen
    Interaktive Graphen   download
    Elementares Übungsblatt Klasse 10

    Besondere Flächeneigenschaften der Potenzfunktionen
    Polynome und ihre Nullstellen

    "Die Kraft der mehrfachen Nullstellen"

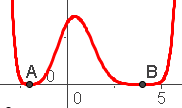    So würde ich gern einmal einen Vortrag nennen. Man kann nämlich aus der Vielfachheit von Nullstellen schon ungeheuer viel über die qualitativen Graphen von Polynomen ausssagen und es ist absolut unmathematisch, bei völlig geklärtem qualitativen Verlauf noch die beliebten Prüfungen mit der 2. und 3. Ableitung zu veranstalten.

    Eine kleine Kostprobe, wie Argumentationen im Unterricht aussehen könnten.

    Dergleichen schriftlich darstellen zu sollen, ist durchaus ein etwas höheres Lernziel.

    Aber auch wenn man i.w. mündlich kommuniziert, findet schönste Mathematik statt und kein stumpfes unverstandenes Kalkül.
    Das rechts dargestellte Polynom muss mindestens 10 Grad haben
    Grund: Das schmalere Minimum ist nicht parabel-ähnlich sondern an der Berührstelle breiter, weiter außen aber wächst es sehr schnell. Darum ist dort eine Nullstelle mindestens 4. Grades.
    Das rechte Minimum ist deutlich "ausgeprägter", muss also mindestens Vielfachheit 6 haben.
    Also ist der Grad des Polynoms mindestens 10.
    Nun sei also der Grad wirklich 10. Dann ist das sichtbare Maximum ein einfachen Maximum 2. Grades. (D.h. würde man die x-Achse dadurch legen, wäre dort eine Nullstelle der Vielfachheit 2.)
    Grund: Die beiden Minima kann man sich zusammengeschmolzen denken aus einer W-Form und einer Doppel-W-Form (zwei Maxima, drei Minima). Insgesamt sind also drei Maxima verschwunden, das hat 6 "Grade gekostet". Läge also im oberen Maximum die x-Achse, dann lägen außen zwei einfache Nullstellen. 2+6=8, zu Grad 10 bleiben nur noch 2, und damit ist das sichtbare Maximum ein Maximum 2. Grades.

    Besonders eindrucksvoll kann man die Zusamenhänge in GeoGebra erkunden:
    Das besprochene Bild dynamisch und Vieta Interaktiv    download

    Vielen ist das Hornerschema bekannt, mit dem man leicht ganzzahlige Nullstellen findet. Aber nicht alle wissen, dass man damit auch die Koeffizienten des "Restpolynoms" findet.
    Dazu eine gute Erklärungsseite zum erweiterten Hornerschema
    Von-Hand-Rechnung als Bild

    Anmerkung: Der Satz von Vieta wird verschieden formuliert. Ich verwende ihn folgender Kurzform: Jede Nullstelle eines Polynoms erzeugt einen "Linearfaktor" (x-nullstelle). Eine r-fache Nullstelle erzeugt den Faktor (x-nullstelle)^r.

    Dieses ist die reelle Variante des Fundamentalsatzes der Algebra": Im Komplexen hat jedes Polynom n-ten Grades genau n Nullstellen.
    Als Vietaschen Wurzelsatz bezeichnet man Betrachtungen über den Aufbau der Koeffizienten, die sich aus dieser Tatsache ergeben. Dergleichen ist eigentlich nach meiner Auffassung kein "Lernstoff", sondern kann stets neu beobachtet, hergeleitet und eingebracht werden.
    Handwerk: Nullstellen bestimmenLeitseite Nullstellen widmet sich den Aussagen über Nullstellen und den Näherungsverfahren.
    Leitseite Gleichungen widmet sich den exakten Verfahren.

    Damit es gleich kar ist:Gleichungen 3. Grades exakt lösen ist ziemlich schwierig und sprengt das übliche Schulniveau. Hier aber geht auch das unter Einbeziehung interaktiver Möglichkeiten.
    Die Biquadratische Gleichungen und ihre Verwandten sind Standard.
    Die allgemeine Gleichung 4. Grades kann man auf den 3. Grad zurückführen.
    Es sollte aber jeder gute Mathematikunterricht beibringen, dass Gleichungen höher als vom 4. Grad nur noch in Sonderfällen zu lösen sind. (Satz von Niels Hendrik Abel) (Sonst wartet noch jemand auf eine Software, die das "endlich" kann.)
  • Polynomschar mit Sehne

    • © Prof. Dr. Dörte Haftendorn
    www.mathematik-verstehen.de
    		 [Analysis]  [Funktionen und Graphen]  [Parabeln]  [Polynome im Affenkasten] [Nullstellen] [Computer] [Numerik] 
    Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Nov. 2002, update 14. Juli 2013         		Site-Info
    Link zum Buch
    www.leuphana.de/matheomnibus       www.doerte-haftendorn.de
    https://mathe.web.leuphana.de     http://www.mathematik-sehen-und-verstehen.de