www.mathematik-verstehen.de
© Prof. Dr. Dörte Haftendorn

Link zum Buch
Site-Info
https://mathe.web.leuphana.de/analysis/affenkasten/affenkasten.htm
[Polynome im Affenkasten]  [Aufgaben]  [Integrale]  [Analysis]  [Computer]  

Polynome im Affenkasten

 Material und Themenseiten
finden Sie weiter unten

Ziele

Wie und mit welchen Möglichkeiten kann man im Standardstoff "Polynome" sinnvollen Mathematikunterricht kann, der den Lernenden eigenes Erkunden ermöglicht?
Schon lange bevor Computer-Algebra-Systeme auf Computern oder Taschenrechnern in der Lage waren, die Rechnungen für eine übliche Kurvendiskussion schnell und exakt auszuführen, war es unerträglich, wenn Schüler jede Aufgabe als neues Problem auffassen sollten. Heute aber ist es unerlässlich, dass wir beibringen, was man bei einem Polynom bestimmten Grades erwarten kann und was nicht gelten kann. Nur so können wir eine sklavische Abhängigkeit von der Maschine verhindern. All zu leicht ist man in der Gefahr, die Deutung von einem Graphen mit unzulänglichen Grenzen oder unpassender Skalierung aus zu versuchen. Durch den Affenkastenbegriff wird eine Vertrautheit mit Polynomen ermöglicht, und diese ist eine wichtige Voraussetzung für wahres Lernen.
Darüber hinaus eröffnen die angeregten Fragestellungen die Möglichkeit, von Hand oder mit Hilfe von Computer-Algebra-Systemen, Zusammenhänge selbst zu entdecken, weitere Ideen und Vermutungen zu verfolgen und so zu mathematisch kreativem Arbeiten zu gelangen.
Grundlegendes mathematisches Vorgehen wird demonstrierbar, wenn die besonderen Verhältnisse bei den schrägen Kästen in beliebiger Lage mit Scherung und Translation auf die leichter beweisbaren geraden Fälle in Normallage zurückgeführt werden.

Wie es zu dem Namen kam

In diesem Thema geht es darum, dass Polynome in Kästen mit gleichmäßigen Abständen eingezwängt sind, dass sie keine Freiheit haben, an anderer Stelle Punkte zu erreichen, als es das Gesetz des Kastens erlaubt. Wenn ich also ein Polynom zeigen will, so präsentiere ich es in seinem Käfig. Das erinnert sehr an die Gaukler und Bader des Mittelalters, die Affen, Bären und andere Tiere in Schaukäfigen oder an Ketten auf den Marktplätzen dem staunenden Publikum vorführten. Ein wenig "exotisch" sind die Polynome für die Schüler ja schließlich auch. Sollen dann im folgenden die Phänomene erkundet, beschrieben und begründet werden, so hat man in dem Begriff des "Affenkastens" ein wahrhaft griffiges Wort, das alle Redeweisen vereinfacht und anschaulich macht. "Anschauung" ist wohl überhaupt die unerlässliche Grundlage für wahres Verstehen und kreatives Arbeiten. Ein ganz wesentlicher Unterschied besteht allerdings zu den Schautieren des mittelalterlichen Gauklers. Für sie bedeutete die Entfernung von Kasten und Kette die Freiheit, Polynome aber stehen unter dem Gesetz des Kastens, auch wenn ihn niemand sieht.

Material

  • Hier ist nun die mit komfortablen Lesezeichen versehene pdf-Datei Polynome im Affenkasten verfügbar. Es beginnt mit einem 50-Seiten-Heft unter diesem diesem Titel, das ich 1995 im Zusammenhang mit allen Begründungen und Beweisen verfasst habe. Es sind nun aber Aufgaben für die freie Erkundung durch Lernende und alle auf dieser Site angebotenen pdf-Seiten eingebunden, inclusive der Folien und Texte zu meinem Vorträgen. Außer mit den Lesezeichen können Sie in dieser Gesamtdatei auch mit Strg F3 komfortabel suchen..
    Die Lesezeichen sehen Sie im Internet-Explorer und natürlich bei Adobe selbst. im Chome und Firefox werden sie leider nicht angezeicht
    Sie dürfen die Ideen nicht an Verlage o.ä. verkaufen, sonst uneingeschränkt nutzen.
    Nochmals: Alle nachfolgenden pdf-Seiten hier dabei. Alledings natürlich nicht die interaktiven Dateien, daher folgen diese in diesem Bereich, manchmal mit den genau passenden pdf-Seiten.
  • Eine Kurzfassung (erstellt für die "Beiträge zur Mathamatikdidaktik 2003")
  • Nachdem ich in diversen Lehrerfortbildungen seit 1996 dieses Thema erst noch mit "echten Folien" vorgetragen hatte, war 2001 für die Mathematische Gesellschaft Hamburg ein Powerpoint-Vortrag entstanden, den ich für die GDM, die MNU und andere Gelegenheiten eingestzt habe. Es ist ja mein "ureigenstes" Thema.
    2009 habe ich für SINUS-Bayern nochmal eine gründliche Überarbeitung gestartet,die vor allem die interaktiven Möglichkeiten von GeoGebra umfassend einsetzt.
    Vortag St. Ottilien 2009      Handzettel    Powerpoint original
    Sie finden aber alle verwendeten GeoGebra-Dateien bei den passenden Unterthemen.

Polynome 3. Grades, Leitseite 
Als Einführung eignen sich die Polynome 3. Grades besser, da sie verschiedene Formen haben können. Da kann man besser Wirkungen studieren. Z.B. verändern sie beim Scheren ihre Form, das tun Parabeln nicht.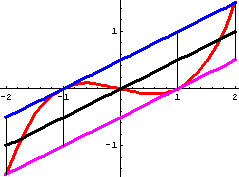
Leitseite Polynome 3. Grades und ihr Affenkasten

Scherung, Leitseite  


Scherung als übergreifendes Beweiselement
Übergreifende Beweisidee:Alle Eigenschaften brauchen nur für -gut ausgewählte- Spezialfälle bewiesen zu werden. Alle anderen Fälle ergeben sich daraus durch eigenschaftserhaltende Abbildungen. Dazu mehr bei Polynomen 3. Grades. Kernidee ist dabei, dass die Addition eines linearen Terms zu einem Funktionsterm geometrisch eine Scherung bedeutet.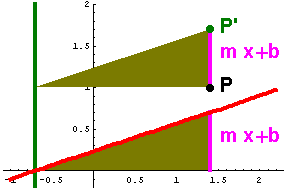

Parabeln, Leitseite 
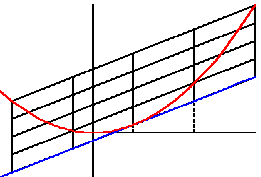Parabeln und ihr Bärenkasten, Leitseite

Polynome 4. Grades, Leitseite


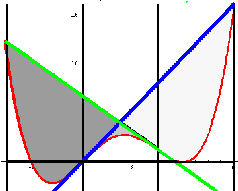Polynome 4. Grades    

Potenzfuktionen, Leitseite 
Flächen bei Potenzfunktionen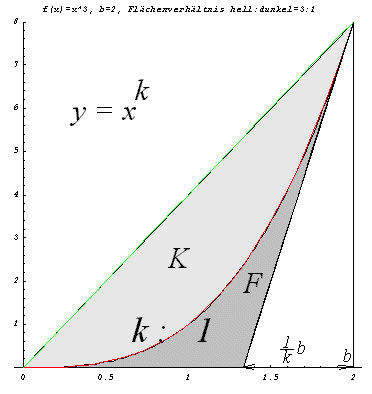

Poly3-Parabel-Ehe
Weitere Besonderheiten: "Parabel-Ehe", eine Aufgabe mit einem Polynom 3. Grades in seinem Affenkasten und den beiden "Wendeparabeln"
Bilder-Aufgabe Galerie 1 Graphen pdf
Bilder-Aufgabe Galerie 2 Flächen pdf
Beides in einer Datei pdf
Einiges zur Lösung pdf
Aufgaben und Klausuren,
die die Affenkasten-Idden aufgreifen.
und nicht einem einzigen der obigen Kapitel zuzuschreiben sind.

Kästen bei e-Funktionen

Auch für andere Funktionenklassen gibt es Kästen
  Schöne Seite zum Eulerkasten "Eulerkasten"
Weitere Weitere Kästen bei e-Funktionen auf der Aufgabenseite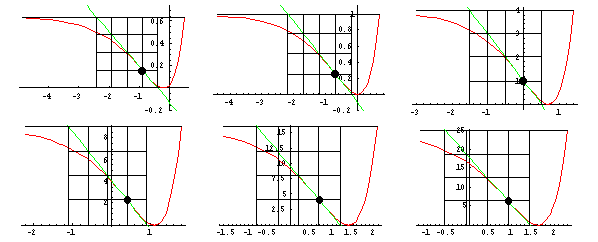

© Prof. Dr. Dörte Haftendorn
www.mathematik-verstehen.de
 [Polynome im Affenkasten]  [Aufgaben]  [Integrale]  [Analysis]  [Computer]  
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  1996 hier neu 2004, update 14. März 2013 		Site-Info
Link zum Buch
www.leuphana.de/matheomnibus       www.doerte-haftendorn.de
https://mathe.web.leuphana.de     http://www.mathematik-sehen-und-verstehen.de