http://haftendorn.uni-lueneburg.de/mathe-lehramt/numerik/numerik.htm[Numerik] [Integrale] [Analysis] [Graphen] [Lineare Algebra]; [Stochastik] [Computer] [MuPAD]
 |
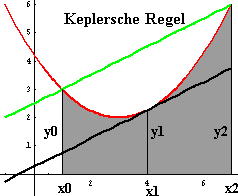
Kepler-Regel und Simpson-Regel
|
 |
 
|
  | |
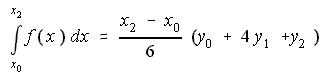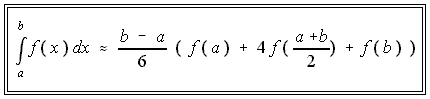 Durch mehrfaches Hintereinandersetzen des Kepler-Doppelstreifens einsteht die Simpsonformel. Aneinander grenzende Doppelstreifen haben dieselbe Ordnate, daher kommen in der Simpsonformel die Faktoren 2 vor. Die Faktoren 4 stammen aus der Keplerformel direkt. Dabei ist h die Breite der Einzelstreifen und man benötigt eine gerade Anzahl Streifen. | |
Parabel im Bärenkasten
, Ausnutzung dieser Idee zum Beweis, Interaktiv beobachten Arbeit mit der Kepler-Regel bei beliebiger Funktion (hier f(x)= x+ cos(x) Arbeit mit der Kepler-Regel bei beliebiger Funktion (hier f(x)= sin(x^2/8) Arbeit mit der Kepler-Regel bei e-Funktion (hier f(x)= e^(-x^3)) Kepler-Regel bringt bei p3 exakte Werte Beweis-Bild, Text dazu in der nächsten Zeile
Parabeln und die Keplersche Regel
Parabeln und die Keplersche Regel
download
[Numerik]
[Integrale]
[Analysis]
[Graphen]
[Lineare Algebra];
[Stochastik]
[Computer]
[MuPAD] |
 Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Okt. 2002, update |
  www.mathematik-verstehen.de www.doerte-haftendorn.dehttp://haftendorn.uni-lueneburg.de http://mathematik.uni-lueneburg.de |
Mit der keplerschen Regel berechnet man das bestimmte Integral einer Funktion durch Verwendung von 3 Stützpunkten. Dabei muss lediglich die innere Stützstelle wirklich der Mittelwert der beiden äußeren sein.