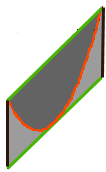
 Archimedes: Quadratur der Parabel
Archimedes: Quadratur der Parabel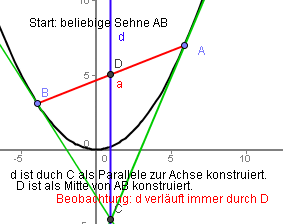
GeoGebra archi1 | Schon lange bin ich auf die besonderen Verhältnisse bei Parabeln und anderen Polynomen gestoßen. Diese habe ich in meinem Schwerpunkt Polynome im Affenkasten zugänglich gemacht.
Bei den Parabeln habe ich "Bärenkästen" gesagt. Mit diesen Erkenntnissen kann man viel anfangen, nicht nur didaktisch. Die Keplersche Integrations-Regel folgt daraus unmittelbar. Aber woher hat Kepler (lange vor Erfindung der Integralrechnung) das gewusst? Antwort: Kepler hat die Werke des Archimedes gekannt, so auch seine Im Folgenden werden gestuft aufgebaute Geogebra-Dateien vorgestellt. Es aber auch die Bilder einsetzbar und erläutert. |
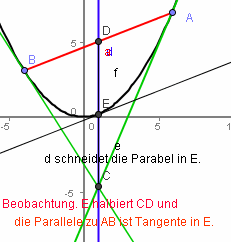 GeoGebra archi2 |
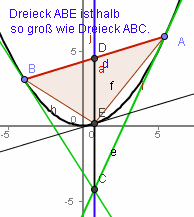 GeoGebra archi3 |
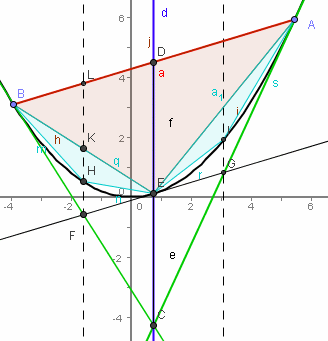
| Hier macht Archimedes
Den entscheidenden Schritt:
Er beginnt die Reste bis zur Parabel mit weiteren solchen Dreiecken auszuschöpfen. Daher heißt dies ausch "Exhaustions-Methode des Archimedes". 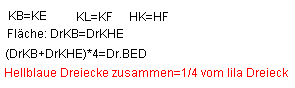 GeoGebra archi4 Interaktiv mit GeoGebra |
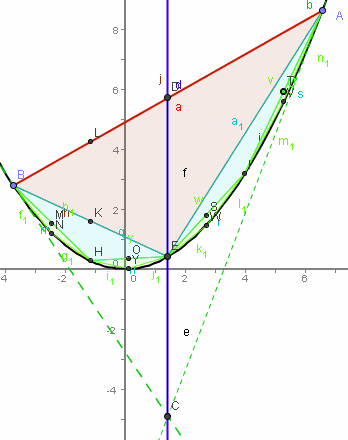
| Nun übernehmen die hellblauen Dreiecke die Rolle, die bisher das lila Dreieck gespielt hat.
Zwei grüne Dreiecke haben alsoein Viertel der Fläche von „ihrem“ hellblauen. 
GeoGebra archi5 Man kann mit den Tangenten in den "Dreicksspitzen" auch eine umfassende Folge erzeugen, die gegen dieselbe Fläche konvergiert. |
| Internetadressen dieses Web-Verbundes [www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt] [haftendorn.uni-lueneburg.de/ing-math] |