https://mathe.web.leuphana.de/analysis/affenkasten/affenkasten.htm[Polynome im Affenkasten] [Aufgaben] [Integrale] [Analysis] [Computer]
|
www.mathematik-verstehen.de |
| |
|
https://mathe.web.leuphana.de/analysis/affenkasten/affenkasten.htm [Polynome im Affenkasten] [Aufgaben] [Integrale] [Analysis] [Computer] | |||
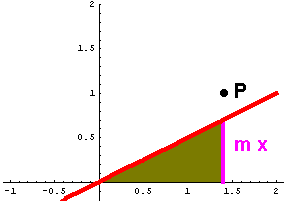
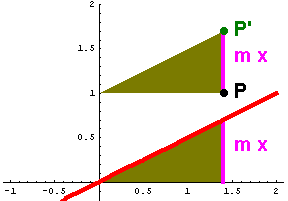
Scherung bei Funktionen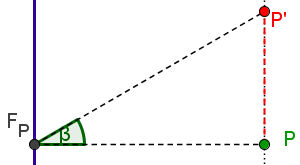 Eine Scherung ist definiert durch die Angabe eine Scherachse g und eines Scherwinkels alpha.
Der Bildpunkt P' eines Punktes P entsteht dadurch, dass P auf einer Parallelen zu g so weit wandert, dass das Lot von P auf die Scherachse um den Winkel alpha kippt.
 Scherung erklären  
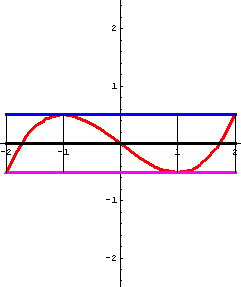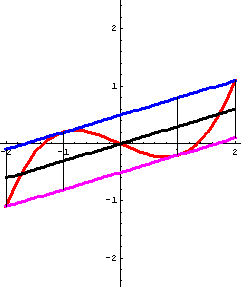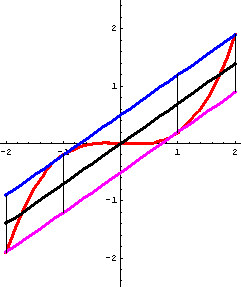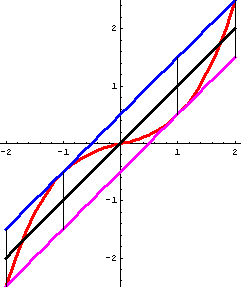
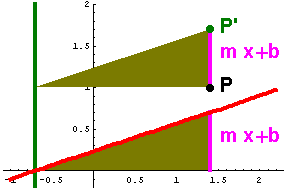
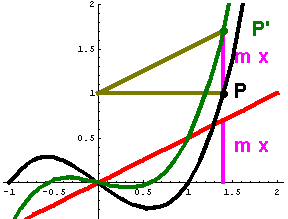
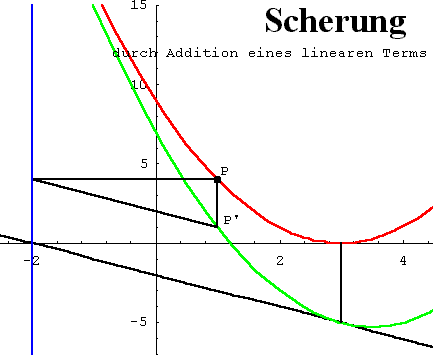
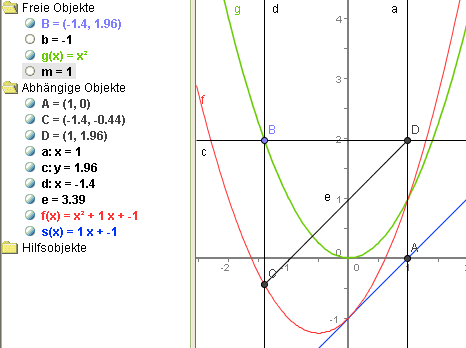
Im Zusammenhang mit Funktionen werden hier nur Scherachsen betrachtet, die zur y-Achse parallel sind. Addition einer Geraden zu einer Funktion bedeutet eine Scherung des Funktionsgraphen. Scherachse ist die Senkrechte durch die Nullstelle der Geraden, Scherwinkel ist der Steigungswinkel der Geraden. 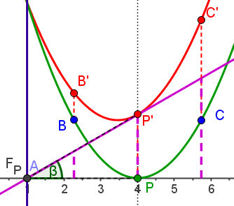 Scherung bei Funktionen erklären
Scherung bei Funktionen (mit Geogebra), Erklärung
Die nachfolgenden Bilder sprechen für sich. Das Scherungs-Argument im Beweiszusammenhang bei den Affenkästen
|  |
 |
 |
 |
 |
 |
|
 |
Stufe 1
  
Stufe 2 
Stufe 3
|
|
|
[Polynome im Affenkasten]
[Aufgaben]
[Integrale]
[Analysis]
[computer]
|
 Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn Nov. 2004, update |
| www.mathematik-verstehen.de www.doerte-haftendorn.de https://mathe.web.leuphana.de http://mathematik.uni-lueneburg.de |
