www.mathematik-verstehen.de		 https://mathe.web.leuphana.de© Prof. Dr. Dörte Haftendorn
URL mathe.web-leuphana.de/algebra/gleichung/cardano.htm
[Algebra]  [Cardano]  [Geschichte] 

Gleichungen 3. Grades

Geschichte Das Lösen von Gleichungen 3. Grades ist mit dem Mathematiker Girolamao Cardano verknüpft.
Nicolo Tartaglia 1499-1557 sah sich eigentlich als Erfinder . Aber schon Scipione del Ferro hatte vorher dazu etwas geschrieben. in http://de.wikipedia.org/wiki/Nicolo_Tartaglia ist die ganze Geschichte so übersichtlich dargestellt, wie man es nach so langer Zeit und erbittertem Streit eben kann. Da man damals noch nicht mit negativen Zalen umgehen konnte, gab es 13 verschiedene Fäle. Erst Cardano löste alle, allerdings z.T. mit dem Wissen seiner Vorläufer. Heute fassen wir diese Methoden i.W. zu einer zusammen und belegen sie mit dem Namen Cardano-Formeln oder cardanische Formeln.
Begründung
Erklärung
Durchführung		 Quadratische Gleichungen wurden schon von Al Khwarizmi mit geometrischer Unterstützung gelöst. Al Khwarizmis Methode ist bei den quadratischen Gleichungen erläutert.
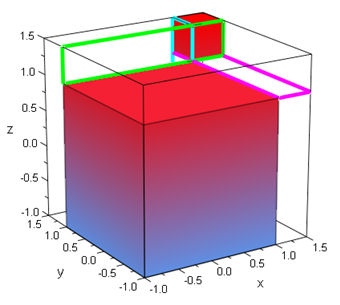
Daher wird hier auch die Lösung von x^3= p x + q durch einen passend aufgeteiltenWürfel angeregt. Würfelidee von Al Kwarizmi  
[Alle Seiten, die dies fortführen, gleich gemeinsam herunterladen ]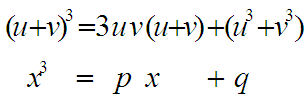

Es wird auf dieser Seite gezeigt, wie man auf eine tri-quadratische Gleichung kommt, deren zwei Lösungen w1 und w2 nun die Grundlage für die 6 Lösungen einer Gleichung 6. Grades werden. werden.
In der folgenden GeoGebra-Datei können alle möglichen Fälle von x^3=p x + q durch Darstellung einer beweglichen Geraden y=p x + q und der Potenzfunktion p(x)=x^3 erfahren werden.
  • Alle Fall-Typen erkunden
  • Auf dieser Seite werden also die -in den meisten Abhandlungen "vom Himmel fallenden"- cardanischen Formeln und Substitutionen begründet.

    • Im Falle "casus irreduzibilis" sind w1 und w2 komlexe Zahlen. Auf der Erklärungsseite zum casus irreducibilis wird ausführlich erklärt, wie man mit Hilfe der dritten Einheitswurzeln alle Lösungen findet.
    Die beiden Zahlen w1 und w2 werden in der folgenden GeoGebra-Datei als Punkte in der Gaußschen Zahlenebene dargestellt, ihre dritten Wurzeln durch Winkeldritteln und Anhängen eines "Mercedes.Stern" geometrisch ermittelt
    Diesen Schritt gibt es extra mit zwei GeoGebradateien:
  • Visualisierung der dritten Wurzeln in der Gaußschen Zahlenebene erstmal mit Betrag 1
  • Visualisierung der sechsten Wurzeln in der Cardanoherleitung

    • Letzlich werden die Lösungen von x^3 =p x + q als Nullstellen des entsprechenden Polynoms dargestellt. Dies alles ist abhängig von interaktiv wählbaren p und q.
  • Interaktives Lösen

    • Selbstverständlich passiert das Winkeldritteln rechnerisch, denn bekanntlich kann man einen Winkel nicht durch Konstruktion dritteln.

    Die einfacheren Fälle, nämlich dass die Diskriminate von w1 und w2 Null oder positiv ist, werden auf der Seite Cardano, einfache Fälle erklärt.
    Auch hierzu gibt es eine GeoGebra-Datei
  • Genau eine relle Lösung
    		•
    TI Nspire
  • Cardano Hauptbeispiel,parallel zu den Erklärungsseiten   Handzettel    download
  • Alle Fälle mit dem TI betrachtet   Handzettel   download
  • In zwei alten Büchern habe ich gefunden, wie man Anfang des 20.Jahrgunderts in den "Gymnasien, Realgymnasien, Oberrealschulen und Gewerbeschulen das Thema "Cadano-Formeln und kubische Gleichungen" unterrichtete.
  • Bardey: "Aufgabensammlung über alle Teile der Elementar-Arithmetik". Leipzig und Berlin 1902 Kompaktversion
  • Heis: Sammlung von Beispielen und Augaben zu allgemeinen Arthmetik und Algebra, Köln 1896
  • Ich danke Rudolf Roolf aus Hilden, der mir diese beiden Bücher geschenkt hat. Sie waren in der Jugend und im späteren Lehrerberuf meines Großvaters Harry Eilers in Gebrauch. Über ihn habe ich leider solche Bücher wegen des Krieges nicht erhalten können. Aber viel wichtiger: Er hat mir seine mathematische Begabung vererbt und meine ersten Schritte in der Mathematik behutsam gefördet.
    • MuPAD Anschauliche Darstellung von Tartaglia mit einem Würfel Die kommentierten Berechnungen und Überlegungen mit dem CAS MuPAD kann amn auch lesen, wenn man MuPAD weder hat noch kennt.
    Gleichungen 3. Grades mit quadratischem Term
    Nun bestimmt man die Nullstellen von f und verschiebt sie um xw zurück.
    Damit ist also jede Gleichung 3. Grades erfasst.
    4.Grades Gleichungen 4. Grades, die weder ganzzahlige Nullstellen haben noch biquadratisch sind, führt man auf auf eine Gleichung 3. Grades zurück, bestimmt deren Nullstellen und daraus dann - falls existent - die vierte. Nullstelle.
    Zuverlässige Seite von Frof. Hebisch, TU Freiberg
    Mit Herrn Hebisch verbindet mich der gemeinsame Doktorvater Prof. Hanns Weinert.
    Die Formeln dafür stehen im Bronstein (nur intern)
    Quasi-
    konstruktion    		Bekanntlich sind 3. Wurzeln nicht mit Zirkel und Lineal konstruierbar. Siehe: Unlösbare Probleme
    Aber bei Erweiterung der Hilsmittel um eine Normalparabel-Schablone gibt es eine
    Lösung der Gleichungen 3. Grades als Quasi-Konstruktion

    [Algebra]  [Gleichungen]  [Geschichte] 
    Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Jan. 2005, update 01. August 2023
    Direkte Internetadressen
    [www.doerte-haftendorn.de]    [mathe.web-leuphana.de]