	www.mathematik-verstehen.de	© Prof. Dr. Dörte Haftendorn
https://mathe.web.leuphana.de/geschichte/griechen/griechen.htm [Kurven] [Geometrie] [Quasi-Konstruktionen] [Geschichte] [Mathematik der Griechen]

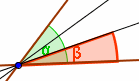Winkeldritteln

Gegeben ist ein Winkel.
Er soll durch eine Konstruktion in drei gleiche Teile geteilt werden.

Unlösbarkeit	Allein mit Zirkel und Lineal gibt es keine Konstruktion! Warum kann man aber nicht doch auf irgendeine Weise den Drittel-Winkel mit Zirkel und Lineal konstruieren? Grundlegendes zu den unlösbaren Problemen der Antike Weiteres zur Mathematik der Griechen
Quasi-Konstruktion	Allgemeines zu Quasi-Konstruktionen mit Zirkel, Lineal und Parabelineal Gleichungen 3. Grades lösen mit Quasikonstruktion als Baustein zum Winkeldritteln Winkeldritteln als Quasi-Konstruktion mit Zirkel, Lineal und Parabelineal
Einpass-Konstuktionen	Winkeldritteln durch Papierfalten Winkeldritteln mit "Tomahawk" download Winkeldritteln mit Einpassen in Parabel download
Konstruktionen mit Höheren Kurven	Winkeldritteln mit der Trisektrix im Projekt Klasse 8
Näherungen	Selbstverständlich kann man einfach die Winkelgröße durch 3 teilen und den Winkel dann zeichnen. Soeine rechnerische Lösung heißt aber nicht "Konstruktion". Es geht eben nicht um das auf diese Weise leicht zu beschaffende Ergebnis, sondern um die geistige Herausforderung, es mit Methoden der Geometrie zu schaffen. Dieser Herausforderung braucht sich aber niemand zu stellen, denn für beliebige Winkel ist die Unmöglichkeit der Drittelung mit Zirkel und Lineal (wie oben ausfühlich begründet) unumstößlich bewiesen. Nähungskonstruktion, die auf der Idee beruhen, dass ein dreigeteilter Winkel aus Kreisen um seinen Scheitel gleichlange Sehnen herausscheiden wird, verleiten zu dem Glauben, man hätte den Winkel mit Zirkel und Lineal gedrittelt. Dann empfiehlt es sich, die Konstuktion in GeoGebra oder Euklid-Dynageo oder einem anden DGS zu realisieren. Da merkt man sofort, dass es nicht stimmt. Inzwischen sind mir zwei solche angeblichen Drittelungen zugeschickt worden: Eine ging mir 2006 zu. Dazu wird eine Sekante mit einem beliebigen Kreis gedrittelt. Es ergeben sich ein zu kleiner und zwei zu große Winkel. Dann wird daraus ein weiterer Kreis konstruiert, bei dem sich ein zu großer und zwei zu kleine Winkel ergeben. Dazwischen muss also der "richtige" Kreis liegen, das ist wahr, und bis hierher auch richtig mit Zirkel und Lineal konstruiert. Nun kommt das Problem: Zwischen zwei sinnvoll gewählten Punkten soll nun eine Gerade mit dem Schenkel des zu teilenden Winkels den Radius dieses Kreises erzeugen. Und genau das klappt nicht und ist auch mit Zirkel und Lineal nicht verbesserbar. Es ergibt sich aber eine Näherungslösung. Gedruckte und erklärte Zeichnung dazu. Die folgende GeoGebra-Datei zeigt den Zusmmenhang. download Eine andere erreichte mich Anfang 2007:(Die Quelle nenne ich ggf. auf Anfrage) GeoGebra-Datei zeigt den Zusmmenhang. download ein Sonderfall mit dem Drittelwinkel, nicht konstruiert. download Hier habe ich mir die Mühe gemacht, analytisch zu zeigen, warum man mit Zeichnungen von Hand ohne Einsatz von Mathematik zu der Meinung, es handele sich um eine Winkeldrittelung, kommen konnte. Winkeldrittelungs-Versuch nach Sch. Buch,in dem das alles (und mehr) dargestellt ist: Bewersdorff: Algebra für Einsteiger, Vieweg 2002, ISBN 3-528-03192-1

Warum kann man aber nicht doch auf irgendeine Weise den Drittel-Winkel mit Zirkel und Lineal konstruieren? Diese Begründung ist als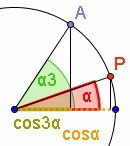

aus der Seite Winkeldritteln als Quasikonstruktion

Überlegung: Will man

aus

bestimmen, dann ist das äquivalent zu dem Bestimmen von

aus

.
Dazu schreibt man mit Hilfe der Additionstheoreme

in Terme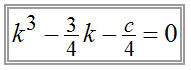n von

Es folgt:

, also:

An dieser Gleichung 3. Grades sieht man, dass die Konstruktion mit Zirkel und Lineal allein nicht klappen kann, denn tiefsinnige Sätze der Algebra (Galois-Theorie) zeigen, dass man damit nur Gleichungen lösen kann, die auf Quadratwurzeln und allenfalls geschachtelte Quadratwurzeln führen.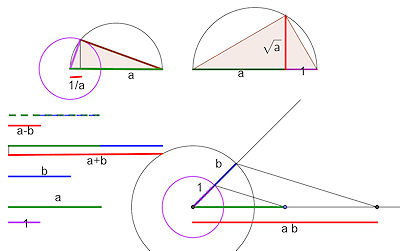

Wenn es zunächst nur ganzzahlige Koordinaten gibt,kann man alle rationalen Zahlen als Koordinaten konstruieren. Endlich viele ,also n, Konstruktionsschritte fühgen allenfalls n Quadratwurzeln hinzu. Genauere Überlegungen zum Konstruieren und den dabei auftretenenden Zahlen

Konstruieren, Erklärungen und Rechnungen

Handzettel

download

Vertiefte Einsicht in Körpererweiterungen, Grundelmente der Galoistheorie

von Hand
Die Gleichungen müssen einen Zweierpotenz-Grad haben, wenn man sie mit Zirkel und lineal lösen will.Jedenfalls nicht Gleichungen Grad 3. Daher kann man einen beliebigen Winkel nicht dritteln

[Kurven] [Geometrie] [Quasi-Konstruktionen] [Geschichte] [Mathematik der Griechen]

Nov. 2004, update 9. Juni 2013

www.mathematik-verstehen.de www.doerte-haftendorn.de
https://mathe.web.leuphana.de http://mathematik.uni-lueneburg.de