	www.mathematik-verstehen.de	© Prof. Dr. Dörte Haftendorn
https://mathe.web.leuphana.de/geschichte/griechen/griechen.htm [Kurven] [Geometrie] [Quasi-Konstruktionen] [Geschichte] [Mathematik der Griechen]

Winkeldritteln

Einpass-Konstruktion als Faltaufgabe	Einpass-Konstruktion mit Tomahawk download	Einpass-Konstruktion mit Parabel download	Winkeldritteln mit der Trisektrix	Winkeldritteln als Quasi-Konstruktion
Grundlegendes zu den unlösbaren Problemen der Antike Quasikonstruktionen

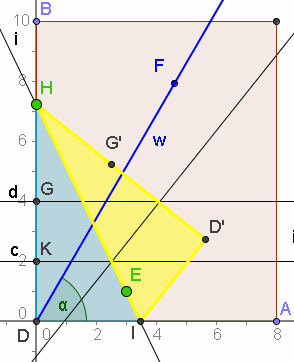	Winkeldritteln als Faltaufgabe: Nimm ein Blatt Papier. Falte in die Ecke D hinein den Winkel, den du Dritteln willst. Der Knick heiße w. Falte unten zwei gleich breite Streifen c und d. Der obere Knick hat am Rand den Punkt G, der untere K. Nimm die Ecke D und falte sie auf c wobei gleichzeitig G auf w zu liegen kommen muss. Hier ist die "Hinfummelstelle", die mann nicht mit Zirkel und Lineal konstruiert bekommt. J sei das Bild von K. DJ ist nun eine Winkeldrittellinie, ebenso DD'.
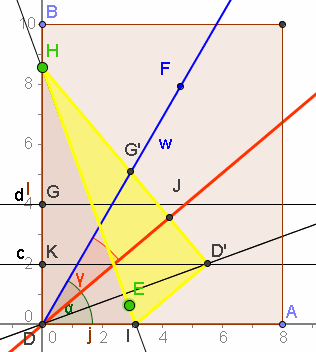	Warum klappt das? DK=r, KG=r, also auch D'J=r und JG'=r. c steht auf DH senkrecht, darum steht auch c' auf D'H senkrecht. Darum ist die rote Gerade c' Mittelsenkrechte im Dreieck D'G'D. Wenn man von D' ein Lot auf die Unterkante fällt, entsteht mit D ein Dreieck, das zum Dreieck DD'J und damit auch zum Dreieck JG'D kongruent ist. Also sind zwischen w und der Unterkante drei kongruente Dreiecke, der Winkel ist gedrittelt.
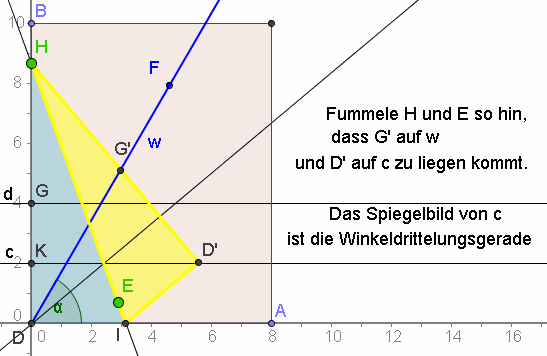Interaktiv mit GeoGebra download

Nov. 2004, update 14. August 2011