© Prof. Dr. Dieter Riebesehl
[Kurven] [Geometrie] [Höhere Geometrie] [Probleme der Antike]
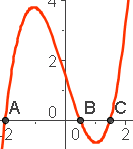     |
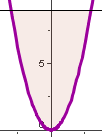 Hier wird nun vorgestellt, wie man durch Hinzunahme eines Parabellineals -also einer Schablone für den Graph der Normalparabel- Quasi-Konstruktionen zur Lösung der allgemeinen Gleichung 3. Grades durchführen kann. Die Parabelschablone ist dabei am Computer realisiert durch die Normalparabel als Kegelschnitt, die sich in GeoGebra mit anderen Kegelschnitten, hier Kreis und Gerade zum Schnitt bringen lässt.
Die so gewonnenen Lösungspunkte lassen sich beliebig weiter verwenden und sie sind mathematisch exakt wie bei den üblichen Zirkel-Lineal-Konstruktionen auch. Daher sprechen wir von einer Quasi-Konstruktion. Sie unterscheidet sich fundamental von Konstruktionen mit "Einpassung" und von Näherungslösungen .
Hier wird nun vorgestellt, wie man durch Hinzunahme eines Parabellineals -also einer Schablone für den Graph der Normalparabel- Quasi-Konstruktionen zur Lösung der allgemeinen Gleichung 3. Grades durchführen kann. Die Parabelschablone ist dabei am Computer realisiert durch die Normalparabel als Kegelschnitt, die sich in GeoGebra mit anderen Kegelschnitten, hier Kreis und Gerade zum Schnitt bringen lässt.
Die so gewonnenen Lösungspunkte lassen sich beliebig weiter verwenden und sie sind mathematisch exakt wie bei den üblichen Zirkel-Lineal-Konstruktionen auch. Daher sprechen wir von einer Quasi-Konstruktion. Sie unterscheidet sich fundamental von Konstruktionen mit "Einpassung" und von Näherungslösungen .
Didaktischer Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn |
https://mathe.web.leuphana.de http://mathematik.uni-lueneburg.de |