© Prof. Dr. Dieter Riebesehl
[Kurven] [Geometrie] [Höhere Geometrie] [Probleme der Antike] [Quasi-Konstruktionen]
 | Diese Seite druckgünstig als | ||
| Hilfsmittel: Zirkel Lineal Parabellineal |
download Herleitung Beschreibung der Konstruktion |
Allgemeines zu den Quasi-Konstruktionen unlösbare Probleme der Antike |
|
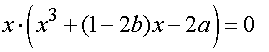
 Konstruktion:
Gegeben sind p und q.
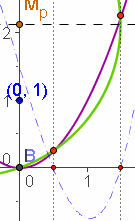
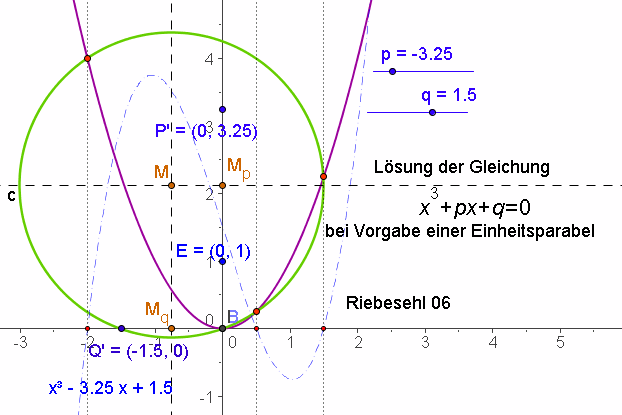
Spiegele P=(0,p) in P'=(0,-p) und Q=(q,0) in Q'=(-q,0). Konstruiere Mp als Mitte von P' und E=(0,1) und konstruiere Mq als Mitte von Q' und (0,0). Konstruiere M aus Mp und Mq mit Senkrechten. Schlage um M den Kreis durch den Ursprung.
Zeichne die Normalparabel y=x^2 ein. (Achtung: y=x^2 wirklich eingeben, dann wird die Parabel als Kegelschnitt erkannt.)
Nun erzeugt man mit dem Schnitt-Werkzeug die Schnittpunkte von Parabel und Kreis. Die Schnittstellen sind die gesuchten Lösungen.
Als Probe kann man die Funktion (gestrichelt) einzeichnen und mit dem Befehl Nullstellen[f] bestätigen sich die konstruktiv erzeugten Stellen.
Konstruktion:
Gegeben sind p und q.
Spiegele P=(0,p) in P'=(0,-p) und Q=(q,0) in Q'=(-q,0). Konstruiere Mp als Mitte von P' und E=(0,1) und konstruiere Mq als Mitte von Q' und (0,0). Konstruiere M aus Mp und Mq mit Senkrechten. Schlage um M den Kreis durch den Ursprung.
Zeichne die Normalparabel y=x^2 ein. (Achtung: y=x^2 wirklich eingeben, dann wird die Parabel als Kegelschnitt erkannt.)
Nun erzeugt man mit dem Schnitt-Werkzeug die Schnittpunkte von Parabel und Kreis. Die Schnittstellen sind die gesuchten Lösungen.
Als Probe kann man die Funktion (gestrichelt) einzeichnen und mit dem Befehl Nullstellen[f] bestätigen sich die konstruktiv erzeugten Stellen.
Didaktischer Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn |
[https://mathe.web.leuphana.de] [http://mathematik.uni-lueneburg.de] |