© Prof. Dr. Dieter Riebesehl
[Kurven] [Geometrie] [Höhere Geometrie] [Probleme der Antike] [Quasi-Konstruktionen]
| Diese Seite druckgünstig als | |||
 | Hilfsmittel: Zirkel Lineal Parabellineal |
download Herleitung Beschreibung der Konstruktion |
Quasi-Konstruktion für Gleichungen 3. Grades Allgemeines zu den Quasi-Konstruktionen unlösbare Probleme der Antike |
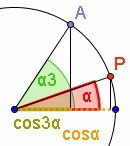
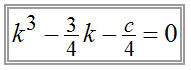
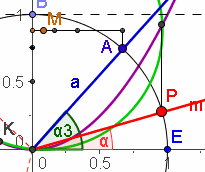 Auf der Seite "Quasi-Konstruktion für Gleichungen 3. Grades" werden Lösungen durch den Schnitt von Kreis und Normalparabel erzeugt. Im Vergleich mit der Cardano-Standard-Form der Gleichung 3. Grades
Auf der Seite "Quasi-Konstruktion für Gleichungen 3. Grades" werden Lösungen durch den Schnitt von Kreis und Normalparabel erzeugt. Im Vergleich mit der Cardano-Standard-Form der Gleichung 3. Grades 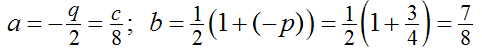 sein.
sein. 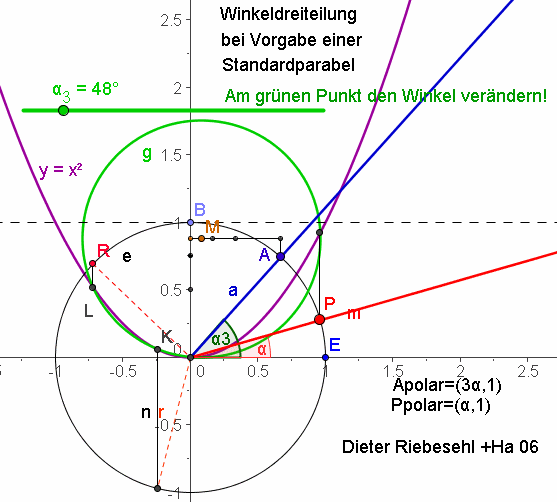 In der GeoGebra-Datei ist die Größe von
In der GeoGebra-Datei ist die Größe von 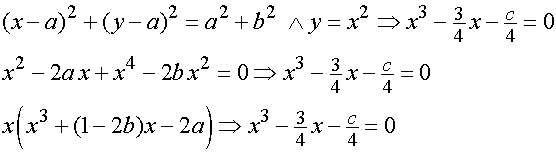
Didaktischer Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn |
[https://mathe.web.leuphana.de] [http://mathematik.uni-lueneburg.de] |