www.mathematik-verstehen.de	https://mathe.web.leuphana.de	© Prof. Dr. Dörte Haftendorn
https://mathe.web.leuphana.de/algebra/gleichung/gleichung.htm [Algebra] [Nullstellen] [Lernpakete] [Geschichte]

Gleichungen

Lineare Gleichungen	Lineare Gleichung interaktiv visualieren, Lösung ablesen download Umformungen einer linearen Gleichung mx+b=px+q interaktiv visualisieren,Lösung bleibt fest download
Lineare Gleichungssysteme	Lineare Gleichungssysteme von Hand
Quadratische Gleichungen	Quadratische Gleichung von Hand Quadratische Gleichungen mit der Normalparabel lösen download Quadratische Gleichung visualisiert nach Al Khwarizmi download Ausführliche Erklärungsseite zu Al Khwarizmi Quadratische Gleichungen geometrisch lösen mit Schiebereglern p und q wählen download Quadratische Gleichungen geometrisch lösen Geometrische Auswahl download Überraschende geometrische Lösung quadratischer Gleichungen (Animierte Herleitung) von Andràs Ringler Universität von Szeged, Ungarn
Allgemeine Gleichungen	Weitere Gleichungen Sek I Am besten stellt man die rechte und die linke Seite der Gleichung als Funktion dar und sieht sich den Schnittpunkt oder Menge der Schnittpunkte numerisch an. Als Werkzeug eignet sich sehr gut GeoGebra, aber auch alle Graphenzeichner und CAS. In manchen Fällen hilft der Begriff "Umkehrfunktion". Siehe auch unten -> exponentielle Gleichungen Die Näherungsverfahrn zur Gleichungslösung befinden sich auf der Seite Nullstellen
Kubische Gleichungen	Sie sprengen den Schulrahmen, wenn es sich nicht um Sonderfälle handelt (siehe bei höhere Polynomgleichungen) Sinnvoll ist die numerische Bestimmung mit GTR oder exakte Bestimmung mit CAS Die exakte Bestimmung hat eine Jahrhunderte alte Tradition, die auf Tartaglia und Cardano zurückgeht: 2011 schöne neue Leitseite mit vollständigen Erklärungen. Auch als sinnvolle anwendung von komlexen Zahlen und Einheitswurzeln insbesondere im Lehramsstudium. Gleichungen 3. Grades mit Cardanischen Formeln Gleichungen 3. Grades geometrisch als Quasi-Konstruktion Schnitt von Kreis und mit Normalparabel
Gleichungen 4. Grades	Sie sprengen den Schulrahmen, wenn es sich nicht um Sonderfälle handelt (siehe bei höhere Polynomgleichungen) Sinnvoll ist die numerische Bestimmung mit GTR oder exakte Bestimmung mit CAS Eine exakte Methode unternimmt eine Rückfürung auf eine Gleichung 3. Grades, aus deren Lösung dann die vierte Lösung (falls existent) bestimmt wird. Die Formeln dafür stehen im Bronstein
Höhere Polynom-Gleichungen	Gleichungen, bei denen die Variable in einem Polynom n-ten Grades vorkommt. Niels Hendrik Abel hat bewisen, dass es keine allgemeinen Lösungsverfahren für Gleichungen vom 5. Grad oder höher geben kann. Diese Gleichungen sind nur dann lösbar, wenn es sich um Sonderfälle handelt. Sonst bleibt nur die numerische Lösung mit GTR oder mit Sekantenverfahren ( im GTR programmiert) oder Newtonverfahren. Fundamentalsatz der Algebra und Vieatascher Wurzelsatz Sonderfall: es existieren ganzzahlige Lösungen: 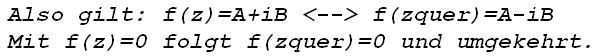Schritt I: Ausklammern soweit möglich Schritt II Suche (mit Horner-Schema, oder dem Graphen) ganzzahliger Nullstellen als Teiler des Absolutgliedes Schritt III Restpolynom aus Hornerschema ablesen (oder Division durch (x-xo))und wiederholen ab Schitt 2 oder Restpolynom=0 als quadratische Gleichung oder mit den oben genannten Methoden lösen. Hornerschema Hornerschema von Hand Nullstellen von Polynomen mit geradem Grad über den reellen Zahlen treten stets paarweise als konjugierte Wurzelausdrücke oder als konjugiert- komplexe Zahlen auf. Beweis (bis Grad 4) (Bild) Polynome mit ungeradem Grad über den reellen Zahlen haben sicher eine reelle Nullstelle. Darüber hinaus treten als Nullstellen stets paarweise konjugierte Wurzelausdrücke oder konjugiert-komplexe Zahlen auf. Weiteres z.B. zu mehrfachen Nullstellen steht auf der Leitseite Polynome
Bruch-Gleichungen	Bei einer Bruchgleichung kommt die Variable in einem oder mehreren Nennern vor. Merke: Multiplziere die Gleichung mit dem Hauptnenner aller vorkommenden Nenner. Wenn die Nenner keinen gemeinsamen Fakltor haben, ist der Hauptnenner das Produkt aller Nenner. Es entsteht eine Gleichung ohne Brüche.
Wurzel-Gleichungen	Erste Wurzeln, Einführung bei Aufbau der Reellen Zahlen Bei einer Wurzel-Gleichung kommt die Variable in einem oder mehreren Wurzeln vor. Merke: "Isolieren - Quadrieren" Zuerst einen Wurzelterm allein auf eine Seite bringen, dann quadrieren. Achtung auf der anderen Seite "Binomi" nicht verpassen. Bleibt dann ein Wurzelterm drin, dann wieder: Isolieren Quadrieren. Achtung die Quadriererei vergrößert die Lösungsmenge. Die enhaltenen Lösungen müssen alle in der Ausgangsgleichung geprüft werden.
Trigonometrische Gleichungen	Bei einer trigonometrischen Gleichung kommt die Variable in einem oder mehreren trigonometrischen Termen vor, also in Sinus, Kosisus, Tangens. Billigfall: Auflösbarkeit nach einem einzigen Term mit trig. Fkt. Dann verwende die Umkehrfunktion davon. Beachte die Mehrdeutigkeit einer solchen Umkehrfrage. Fall,in dem man alles mit einer!!! Trig. schreiben kann unter Verwendung von sin^2(x)+cos^2(x)=1 und tan(x)=sin(x)/cos(x). Z.B. schreibe alle mit sin(x), setze z:=sin(x) und löse mit üblichen Methoden. , dann: Billigfall. Harter Fall: tranzendente Gleichung, s.u.
Exponentielle und logaritmische Gleichungen	Exponential-Gleichungen sind solche, bei denen die Variable in den Exponenten vorkommt. Merke: Logarithmiere beide Seiten mit einem beliebigen Logarithmus, (Schule: lg, Sek II, Wissenschaft ln) Logarithmusgleichungen: wende auf beiden Seiten die passende Exponentialfunktion an. Hierzu im Füllhorn Sek I Seiten 28 bis 32 Harter Fall: transzendente Gleichungen. z.B. e^x und freies x.
Transzendente Gleichungen	Das sind solche in denen die Variable sowohl in tranzendenten Fkt (trigon. Fkt, Exponential-Fkt, Log-Fkt) als auch frei oder in verschiedenen solchen vorkommt. Merke: Tranzendente Gleichungen lassen sich nur in ganz seltenen Sonderfällen exakt lösen. Meist muss man zu numerischen Methoden greifen. (Sekantenverfahren, Newtonverfahren, Computerwerkzeuge) Eine interessante Transzendente Gleichung, Extraseite
Differential-Gleichungen	Hierzu eigene Leitseite Differntialgleichungen
Vektor-Gleichungen	Hierzu eigene Leitseite Lineare Algebra
Mehr zu Gleichungen und Nullstellenbestimmung	Mehr zu Nullstellen bestimmen und Gleichungen lösen