www.mathematik-verstehen.de
[Algebra] [Gleichungen] [Nullstellen] [Lernpakete] [Geschichte]
| Anlass | Der Lehrer Jürgen Sonnemeyer schrieb mir (April 08) Beim TI 92 habe ich folgenden interessanten Fehler gefunden. Als Lösungen der Gleichung 2^x-x2-1=0 werden 0 und ca. 4,257 angegeben. Der Fehler ist interessant, weil die relativ einfache Lösung 1 nicht gefunden wurde, ein kleines Beispiel, dass der Mensch der Technik (noch?) in manchen Fällen überlegen ist. Woher ich die Gleichung habe, weiss ich nicht mehr. |
| TI voyage | 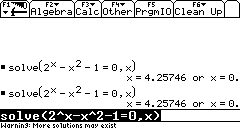 Auch der TI voyage zeigt nur die beiden äußeren Lösungen. Auch der TI voyage zeigt nur die beiden äußeren Lösungen. Allerdings erscheint eine Zeile: Warning, more solutions may exist. Genau, das ist es eben. Leider verschwindet diese Anzeige nach wenigen Sekunden. |
| Graphisch | 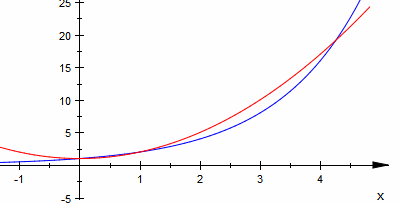 Meine Antwort: Meine Antwort:Ihr Beispiel für die Gleichung zeigt auch, dass man eigentlich immer denken und auch zeichnen sollte. Als Schnittproblem formuliert ist ja klar, dass die Exponentialfkt die Parabel für x=0 wirklich schneidet und nicht nur berührt. Da es noch die Schnittstelle 4,... gibt, muss!!! es noch eine weitere Schnittstelle geben. Ich finde auch immens wichtig, dass man klärt, dass eine solche transzendente Gleichung ja nur numerisch gelöst werden kann. |
| Testen | Ich habe dann mal probiert, was die anderen CAS damit machen: |
| TI nspire | Aha, da sind nun alle Lösungen da. Allerdings kann man lediglich an den Punkten hinter 0 und 1 erkennen, dass der TI auf Numerik umgeschwenkt ist. |
| MuPAD 4 |  MuPAD lehnt die exakte Lösung der transzendenten Gleichung sinnvollerweise ab. Mit Numerik erhält man nur eine Lösung, wenn man keine weiteren Angaben macht.Die anderen findet man bei passender Einschränkung. MuPAD lehnt die exakte Lösung der transzendenten Gleichung sinnvollerweise ab. Mit Numerik erhält man nur eine Lösung, wenn man keine weiteren Angaben macht.Die anderen findet man bei passender Einschränkung. |
| Mathematica 5.2 |
 Mathematica gibt noch Hinweise, woran es liegt, dass keine keine algebraische Lösung gefunden werden kann. Mathematica gibt noch Hinweise, woran es liegt, dass keine keine algebraische Lösung gefunden werden kann. Für diesen Gleichungstyp muss man FindRoot nehmen. |
| Derive 6 | 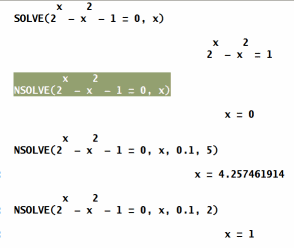 Entsprechnend wie MuPAD Entsprechnend wie MuPAD |
| Maple 8 | 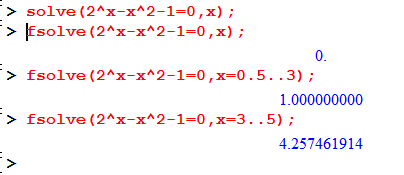 Ebenso, auch hier kein Hinweis. Ebenso, auch hier kein Hinweis. |
|