www.mathematik-verstehen.de © Prof. Dr. Dörte Haftendorn		Link zum Buch Site-Info
	URL haftendorn.uni-lueneburg.de/mathe-lehramt/analysis/polynome/vieta-wurzelsatz.htm [Analysis]  [Funktionen und Graphen]  [Parabeln]  [Polynome]  [Polynome im Affenkasten]  [Nullstellen]  [Computer]  [Numerik]

Fundamentalsatz und Vietascher Wurzelsatz

Fundamentalsatz	Der Fundamentalsatz der Algebra besagt, dass sich ein Polynom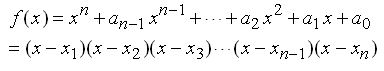 n-ten Grades stets als Produkt von n Linearfaktoren der Gestalt (x-xk)schreiben lässt, wobei xk alle n komplexen Nullstellen durchläft. Vortrag von Prof. Dr. Dieter Riebesehl, Leuphana Universität Lüneburg auf der Tagung GDM und DMV in Berlin 2007 Zusammenfassung Powerpointvortrag z^3 als Abbildung eines Kreises Element des 3. Beweises von Gauß zum Fundamentalsatz Kubisches Polynom bildet einen Kreis ab Nullstellen von Polynomen mit geradem Grad über den reellen Zahlen treten stets paarweise als konjugierte Wurzelausdrücke oder als konjugiert- komplexe Zahlen auf. Beweis (bis Grad 4) (Bild) Polynome mit ungeradem Grad über den reellen Zahlen haben sicher eine reelle Nullstelle. Darüber hinaus treten als Nullstellen stets paarweise konjugierte Wurzelausdrücke oder konjugiert-komplexe Zahlen auf.
Vietascher Wurzelsatz	Multipiziert man diese Klammern aus, so ergibt sich ein Zusammenhang zwischen den Koeffizienten aj und den Nullstellen xk Im Folgenden werden die Polynome nach ihrem Grad sortiert betrachtet.
Geraden	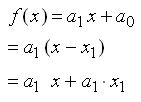in der Darstellung y= m x + b ist also b das negative Produkt aus Steigumg m und Nullstelle x1. Im Folgenden werden alle Polynome normiert, d.h. der höste Koeffizient ist 1.
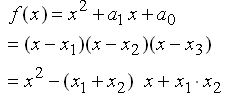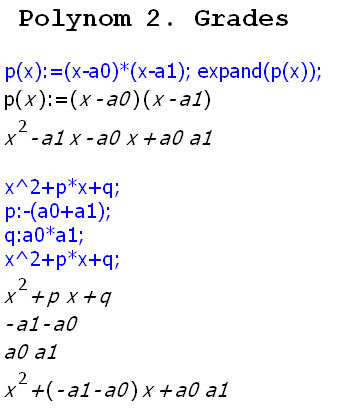
Parabeln	Vietascher Wurzelsatz für Parabeln: Man kann dies verwenden, um ganzzahlige Lösungen zu raten. Da Lösungen die Gestalt s ± Wurzel(r) haben, ist der Faktor vor x, also a1, das Doppelte der Scheitelstelle s und stets reell, auch wenn die Parabel keine rellen Lösungen hat. In diesem Fall sind aber die beiden Lösungen konjugiert-komplex, ihr Produkt ist reell, nämlich a0 = s^2+r^2.
Polynome 3. Grades	Vietascher Wurzelsatz für Polynome 3. Grades Hier treten also die Summe der Lösungen, die Summe aus den drei Produkten aus zwei Löungen und als a0 das Produkt aller drei Lösungen auf. Die letzte Erkenntnis ist nützlich, wenn man ganzzahlige Lösungen raten will. Die weiteren Lösungen findet man dann mit dem Hornerschema und durch Division durch (x-x1) gefolgt vom Lösen einer quadratischen Gleichung. Im Allgemeinen schafft man man aber das Auffinden von Lösungen auf diesem Wege nicht. Siehe dazu die Leitseite Gleichungen 3. Grades (Cardano)
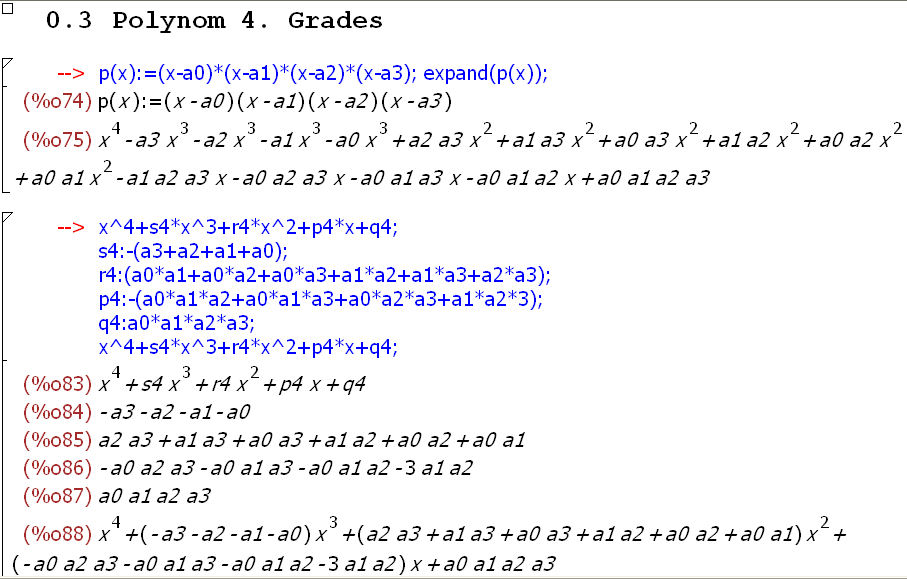
Polynome 4. Grades	Vietascher Wurzelsatz für Polynome 4. Grades Für das Raten gilt das Obige, sonst hat man mit diesen Erkenntnissen wenig Chancen, denn sie führen auf ein nichtlineares Gleichungesastem.
Höhere Grade	Man sieht, wie der Vietascher Wurzelsatz aufgebaut ist. Exakte gannzzahlige Lösungen findet man (und die CAS tun das auch) aus der Produktdarstellung des Absolutgliedes, wenn sie existieren. Für allgemeine Lösungen kann es nach Niels Hendrik Abel kein Verfahren geben. Siehe auch Leitseite Gleichungen
Vielfachheit	Die Konzentraiition auf die reellen Nullstellen, die einfach, doppelt, dreifach u.s.w. sein können ist für den Unterricht höst sinnvoll. Dieses wird auch mit dem NAmen von Vieta verbunden. Siehe auf der Polynom-Seite

© Prof. Dr. Dörte Haftendorn www.mathematik-verstehen.de	[Analysis]  [Funktionen und Graphen]  [Parabeln]  [Polynome]  [Polynome im Affenkasten]  [Nullstellen]  [Computer]  [Numerik]  Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  1996 hier neu 2004, update 14. Juli 2013	Site-Info Link zum Buch
	www.leuphana.de/matheomnibus       www.doerte-haftendorn.de https://mathe.web.leuphana.de     http://www.mathematik-sehen-und-verstehen.de