www.mathematik-verstehen.de
http://haftendorn.uni-lueneburg.de/mathe-lehramt/numerik/interpolation/interpolation.htm[Numerik] [Integrale] [Analysis] [Graphen] [Lineare Algebra] [Stochastik] [Computer] [MuPAD]
 |
Interpolation
|  |
| Interaktiv | Interaktive Dateien zu den nachfolgend beschriebenen Konzepten |
| Parabel |  Parabel durch freie-Punkte  [mehr zu Paraben] |
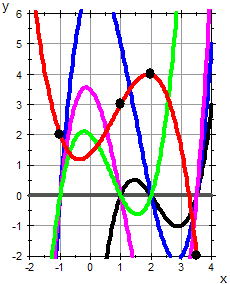
| Polynome, die vorgegebene Punkte treffen | Ein Polynom n-Grades kann durch n+1 Stützpunkte exakt gelegt werden, wenn keine zwei dieser Punkte dieselbe Stützstelle aber unterschiedliche Stützwerte haben. (Klar, das widerspäche dem Funktionsbegriff.) Ein solches Polynom heißt "Interpolations-Polynom". Für seine Beschaffung existieren (mindestens) zwei gute Konzepte: Newtons Interpolationspolynom und das Lagrange-Interpolationspolynom. Weil beide Konzepte eine Basis im n+1-dimenstionalen Vektorraum der Polynom bis zum n-ten Grad aufbauen, ist das Interpolationspolynom durch die n+1 Punkte eindeutig bestimmt. Das Newton-Interpolationspolynom ist identisch mit dem Lagrange-Interpolationspolynom. Die Vorträge unten befassen sich mit diesen Aspekten. Die mathematische Einsicht geht dabei aber über Elementares nicht hinaus. Außerdem kann man das kaum für interaktive Dateien verwenden, da sich mit dem solve-Befehl zuviele Sonderfääe ergeben, wenn die Punktkoordinaten Parameter sind. Die Konzepte von Newton und Lagrange lassen den interassenten mathematisch Begriff "Basis-Polynome" fruchtbar werden und sie lassen sich, wie man auf dieser Seite sieht, für freie interaktive Dateien nutzen. [mehr zu Polynomen] |
| Konzepte | Interpolation nach Newton und nach Lagrange u.a. |
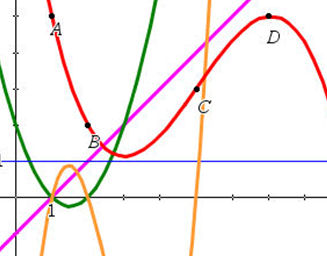
| Newton-Interpolation | Newton baut eine Basis auf, die schrittweise immer mehr der Stützpunkte einbezieht. Das Interpolationspolynom ist dann also eine Linearkombination aus diesen Basispolynomen. Hier müssen die Koeffizienten schrittweise bestimmt werden. Dafür kann man leicht einen Punkt hinzufügen. Polynom durch 6 frei ziehbare Punkte
Diese Datei ist nach dem Konzept von Newton aufgebaut. Daher ist es möglich, sie auch für Polynome durch weniger Punkte zu gebrauchen. Man muss dann nur n(x) deaktivieren und ein passendes der hi anzeigen. Man kann also ohne Punkt F Funktion h4 nehmen, ohne die Punkte F und E gilt h3 u.s.w..  Newton-Interpolation Handzettel download   Newton-Interpolations-Polynom mit Mathematica  |
| Lagrange- Interpolation | Lagrange baut eine Basis so, dass jedes Basispolynom an genau einer der Stützstellen keine Nullstelle hat, an den anderen aber sicher eine Nullstelle hat. Offensichtlich sind diese Grundpolynome linear unabhängig. Sie bilden eine Basis. Das Interpolationspolynom ist dann also eine Linearkombination aus diesen Basispolynomen. Hier kann man die Koeffizienten "in einem Rutsch" aus Formeln bestimmen. Dafür muss man bei Hinzufügung eines weiteren Punktes von vorne anfangen. Lagrange-Polynom durch 4 freie-PunkteLagrange-Interpolation durch 4 freie Punkte Handzettel downloadModellierung der Kostenfunktion, weitere WirtschaftsfunktionenModellierung der Kostenfunktion, weitere Wirtschaftsfunktionen Handzettel download Lagrange-Interpolations-Polynom 
Version in MuPAD 3 als |
| Übergreifend | Angepasste Polynomraum-Basis [mehr zu Vektoräumen]
Basisbegriff in Polynom-Vektorräumen Handzettel download Paderborn, 2013
Kurzaufsatz dazu
Zugehörige interaktive Dateien thematisch bei Interpolation  und bei Splines Handzettel download Basis-Polynome im Polynomraum
|
|
[Numerik]
[Integrale]
[Analysis]
[Graphen]
[Lineare Algebra]
[Stochastik]
[Computer]
[MuPAD]
| |||
| Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn Mai 2007, update | |||
|