www.mathematik-verstehen.de © Prof. Dr. Dörte Haftendorn		Link zum Buch Site-Info
	URL https://mathe.web.leuphana.de/analysis/affenkasten/affenkasten.htm [Analysis] [Nullstellen] [Computer]

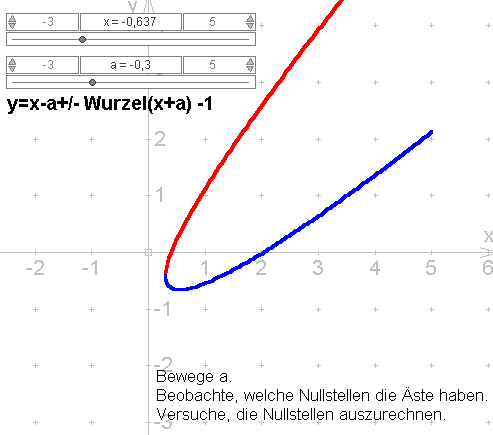
Nullstellensuche ist auch mit CAS nicht billig

Geometrische Version einer Idee von Dr. Hans Schneebeli (Schweiz)

Anzeige der interaktiven Version nur mit Internet-Explorer

Mit den Schiebereglern kann man a variieren.
Dann gleitet die schräge Parabel parallel zu ihrer Achse.
Kernfrage von Hans Schneebeli ist: Welche Nullstellen gibt es (speziell für den roten Ast), in Abhängigkeit von a?
Wie bewältigt ein CAS die Fragen und Prüfungen?

Es stellt sich heraus, dass auch mit CAS die Bestimmung der Nullstellen durchaus nicht trivial ist, ja dass die Einsetzproben nicht ohne Weiteres auf die erwarteten Nullterme führen.
Bei näherem Zusehen stellt sich dieser "Mangel" des CAS aber als mathematisch vernünftig heraus.
Besonders aber ist es sinnvoll die Graphen für verschiedene a zu betrachten, entweder interaktiv (siehe rechts) oder als Kurvenschar, (siehe unten)

Interaktiv mit Dynageo

Hans Schneebelis CAS-Test
dazu noch Graphen: Dörte Haftendorn 25.01.04
Erstaunliche Verpackung der Null

t:=sqrt(-2*(3*sqrt(5)-23))-3*sqrt(5)+1

simplify(t)

float(t)

radsimp(t) //kürzt den nächsten Befehl ab.

simplify(t,sqrt)

Fazit 1: Mit dem passenden Vereinfachungsverfahren gelingt das Herauskitzeln
des mathematischen t-Wertes, der Null.
----------------------------------------------------
Betrachtung zweier Funktionen dieser Bauart
Auffassung: ff und gg als Fkt-Äste der algebraischen
Kurve (y-x+a+1)^2=x+a

ff:=x->(x+sqrt(x)-1);gg:=x->(x-sqrt(x)-1);

plotfunc2d(ff(x),gg(x))

Damit sind pro Ast eine Nullstelle zu erwarten. Ein Lösungsverfahren von Hand wird beide
Lösungen aufeinmal herausgeben, da man auf dem Lösungsweg notwendigerweise
quadrieren muss und damit den Unterschied zwischen ff und gg eliminiert.

fflo:=solve(ff(x)=0,x) //Hier wird schon richtig zugeordnet.

gglo:=solve(gg(x)=0,x)

Einsetzprobe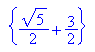

ff(fflo)

Nun entstehen solche Terme wie das eingangs genannte t.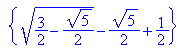
Die Frage ist also, ob das vom CAS passend vereinfacht wird:

simplify(ff(fflo))

Es reicht das schlichte Vereinfachen.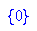
Es scheint zu gelten

glei:=sqrt(x-a)-a+x-1=0

subs(subs(glei,x=3/2),a=sqrt(5)/2)

Entsprechende Funktionen mit Parameter: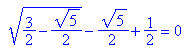

f:=x->(x-a+sqrt(x+a)-1);g:=x->(x-a-sqrt(x+a)-1);

Hier wäre dann die Nullstellensuche interessant: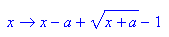

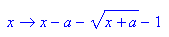
solve(f(x)=0,x)

Das sieht wild aus, nochmal mit Einschränkung auf reelle x und reellen Parameter a: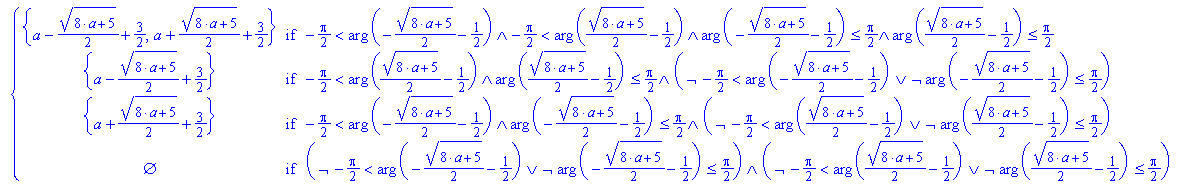

assume(a,Type::Real);assume(x,Type::Real);

solve((x-a+sqrt(x+a)-1)=0,x)

Das ist ja noch unübersichtlicher. Immerhin ist zu erkennen, dass a= - 5/8 einen Grenzfall darstellt.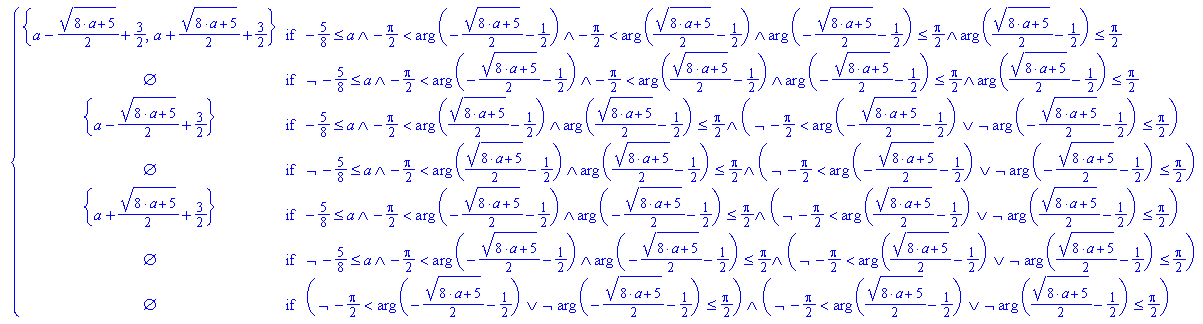
Überblick durch Graphen

plotfunc2d(subs(f(x),a=-1),subs(f(x),a=-5/8),subs(f(x),a=-9/16),
subs(f(x),a=-1/2),subs(f(x),a=0),subs(f(x),a=1),subs(g(x),a=-1),
subs(g(x),a=-5/8),subs(g(x),a=-9/16),
subs(g(x),a=-1/2),subs(g(x),a=0),subs(g(x),a=1),x=-1..2)

Nun kann man sehen, dass es sich um schräg liegende Parabeln (quadratische Form) handelt,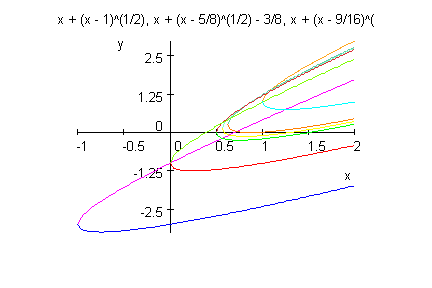
Sicher gilt folgende Übersicht:
a< -5/8 über der x-Achse liegen, also keine Nullstelle haben, für
-5/8 =a hat der untere Ast (g-Ast) eine doppelte Nullstelle
-5/8 < a <c mit noch unbekanntem c hat der untere Ast (g-Ast) zwei verschiedene Nullstellen
a=c muss der Parameter sein, für den der Nahtpunkt zwischen f-Graph und g-Graph auf die x-Achse fällt.
c<a haben dann der f-Ast und der g-Ast je eine Nullstelle.

Bestimmung des Paramterwertes c
f hat als linke Grenze des Definitionsbereiches xmin= - a.
Die Ordinate dazu ist

f(-a)

c ist der Parameterwert, für den diese Ordinate Null wird: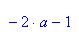

c:=-1/2

Graphen für f und g bei diesem Parameterwert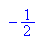

plotfunc2d(subs(f(x),a=-1/2),subs(g(x),a=-1/2),x=-1..4, AxesOrigin=[0,0])

Diverse Proben:

f(x)

subs(f(x),a=-1/2)

lo2(-1/2)

subs(f(lo2(a)),a=-1/2)

f(lo2(a))

e:=a->simplify(f(lo2(a)),sqrt): e(a)

e(7)

Oh je, die beiden a werden nicht identifiziert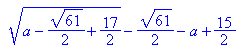

f(lo1(a))

Das sind also die Ordinaten der Möchte-Gern-Nullstellen(a).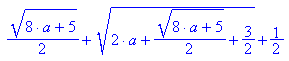
Also direkte Definition:

e:=a->sqrt(2*a-sqrt(8*a+5)/2+3/2)-sqrt(8*a+5)/2+1/2;
eo:=a->sqrt(2*a+sqrt(8*a+5)/2+3/2)+sqrt(8*a+5)/2+1/2;

simplify(e(a),sqrt) //bringt nichts

e(-1/2) //wie erwartet

p1:=plot::Function2d(e(a),a=-5/8..-1/2):
plot(p1,AxesOrigin=[0,0]); // hier keine Nullstellen von f
p1o:=plot::Function2d(eo(a),a=-5/8..1/2):
plot(p1o,AxesOrigin=[0,0]);

p2:=plot::Function2d(e(a),a=-1/2..1):plot(p2,AxesOrigin=[0,0])

plot(p1,p1o,p2)

Fazit: Es zeigt sich, dass obere Ast (f-Ast) der gegebenen Relation
genau für -1/2 <= a Nullstellen hat.

lo1:=a->a+3/2+sqrt(8*a+5)/2;lo2:=a->a+3/2-sqrt(8*a+5)/2

plotfunc2d(lo1(a),lo2(a),a=-1..6,y=0..3)

Dies zeigt, dass die Nullstelle nicht dicht an den Ursprung herankommt,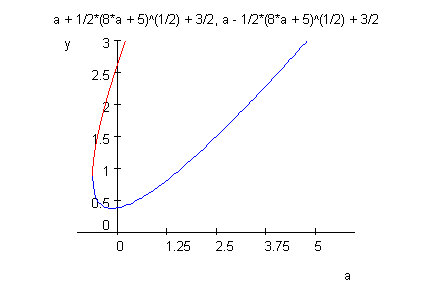
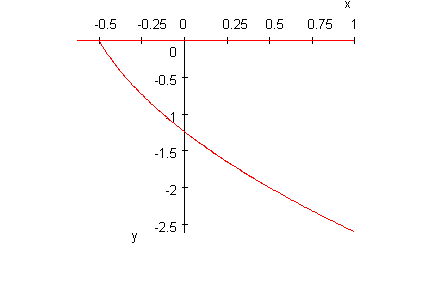
hier ist die Ordinaten-Achse die x-Achse des Ausgangsproblems.

Untersuchungen zum unteren Ast (g-Ast) der der gegebenen Relation

g(lo2(a)); g(lo1(a));

eg:=a->-sqrt(2*a-sqrt(8*a+5)/2+3/2)-sqrt(8*a+5)/2+1/2;
ego:=a->-sqrt(2*a+sqrt(8*a+5)/2+3/2)+sqrt(8*a+5)/2+1/2;

p1g:=plot::Function2d(eg(a),a=-5/8..1/2):
plot(p1g,AxesOrigin=[0,0]); // hier keine Nullstellen von f
p1go:=plot::Function2d(ego(a),a=-5/8..1):
plot(p1go,AxesOrigin=[0,0]);

p2g:=plot::Function2d(eg(a),a=-1/2..1):plot(p2g,AxesOrigin=[0,0]);

plot(p1g,p1go,p2g);

Fazit für den g-Ast der der gegebenen Relation :
Die durch ego repräsentierte Lösung ist für alle -5/8 <= a wirklich Lösung.
Die durch eg repräsentierte Lösung ist nur im Bereich -5/8<=a<= -1/2 wirklich Lösung.

subs(g(lo1(a)),a=-5/8);subs(g(lo2(a)),a=-5/8); //sichert "=" ab

Damit ergibt sich genau das Verhalten, dass man durch die Btrachtung der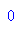
Graphen der gegebenen Relation erschließen konnte.
Die Behandlung des Problems zusammen mit den Graphen halte ich für mathematisch
ergiebiger als die Betrachtung der Gleichungen un Ihrer Lösungen allen.
Wennschon CAS, dann auch CAS als Graphenzeichner.

© Prof. Dr. Dörte Haftendorn www.mathematik-verstehen.de	[Analysis] [Computer] Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn Nov 2002, update 15. August 2011	Site-Info Link zum Buch
	www.leuphana.de/matheomnibus www.doerte-haftendorn.de https://mathe.web.leuphana.de http://www.mathematik-sehen-und-verstehen.de