Mathematik-Verstehen: Wachstum und Zerfall, Modellierung in der Mathematik

	www.mathematik-verstehen.de	© Prof. Dr. Dörte Haftendorn
Anwendungen] [Rekursion] [Folgen] [Funktionen und Graphen] [Differenzialgleichungen]

Wachstum und Zerfall
Modellierung in der Mathematik

Grundlagen im Schulbereich	Erfahrungsgemäß machen sich unsere Studis nicht richtig klar, wie breit auch begrenztes und logistisches Wachstum in Schulbüchern verankert ist. Lesen Sie dazu z.B. "Elemente der Mathematik Klasse 10" Schroedel Ausgabe 1996. Sollten Sie es nicht besorgen können, schicke ich Ihnen auf Email-Anfrage eine pdf-Version der Seiten 108 bis 121. Allgemein ist zu zu bedauern, dass sie die Spinnwebdarstellung in den Schulen nicht immernoch nicht etabliert hat, obwohl ich und andere sie schon seit 1976 kennen und verwenden.
	Unkraut-Ex, eine Beispiel zum Begrenzten Wachstum, i.w. Art Klasse 10 Logistische Parabel mit TI-nspire Erklärungen zum TI-voyage stehen auf der Steite Folgen -> Werkzeuge
GeoGebra	Spinnwebdarstellung rekursiver Folgen mit GeoGebra download Neue Version 07
MuPAD	Folgen, Mengen, Listen
Logistisch	Logistische Parabel
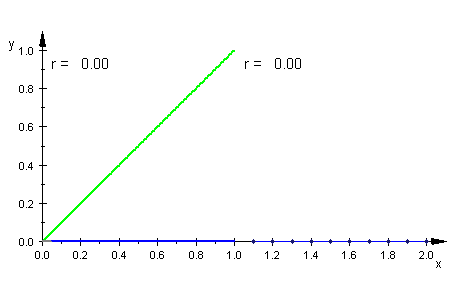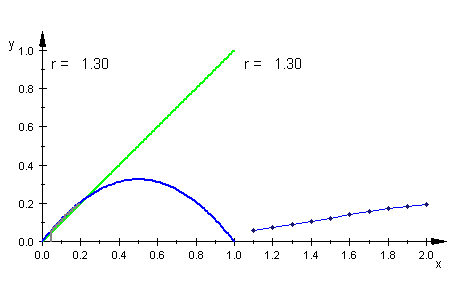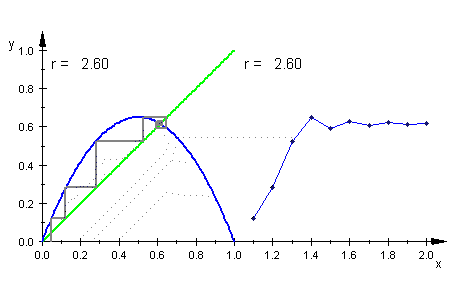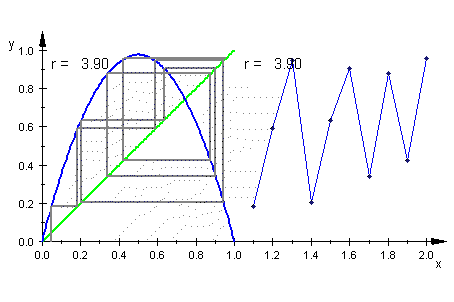
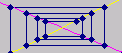Excel	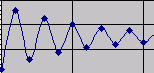Schöne Datei umd allen Wachstumstypen und mit Schiebereglern als download Pardon, Excel übersetzt nicht anständig ins Web Gemeinsame Darstellung der üblichen Zeit-Graphen und der Spinnwebgraphen. Datei ist fertig zum Einsatz, eher in einer Lehrsituation.
Vergleich linear- exponentiell	Judaspfennig Judaspfennig als download Pardon, Excel übersetzt nicht anständig ins Web
Aufgabe	Mathix und sein Konfi-geschenk Handzettel im Webplayer download
Unterricht	Für die freie Arbeit von Lernenden im Thema Wachstum ist Turboplot ausgezeichnet geeignet Umschaltbar zwischen den üblichen Zeit-Graphen und der Spinnwebgraphen. Dazu ist auch das Attraktor-Diagramm (=Feigenbaum-Diagramm) und die Betrachtung der Iterierten möglich. Unterrichtliche Einführung der Spinnwebdarstellung Übungen und Erklärungen zur Spinnweb-Darstellung
Euklid- Dynageo	logistische Parabel mit Euklid-Dynageo (IE erfoderlich)