www.mathematik-verstehen.de © Prof. Dr. Dörte Haftendorn		Link zum Buch Site-Info
	URL  https://mathe.web.leuphana.de/analysis/folgen/folgen.htm [Analysis]  [Computer]

Download des MuPAD-Notebooks     Save Link Taget As..., Verküpfung speichern unter... Rekursive Folgen mit MuPAD,
Parabel-Beispiel Erkundungsaufgabe (pdf)
Prof. Dr.Dörte Haftendorn, April 03,
--------------------------------------------------------------

• f:=x->(-a*(x-2)^2+4)

• a:=1/2:  plotfunc2d(f(x),x,x=-2..4, Scaling=Constrained);
  delete( a):

Fixpunkte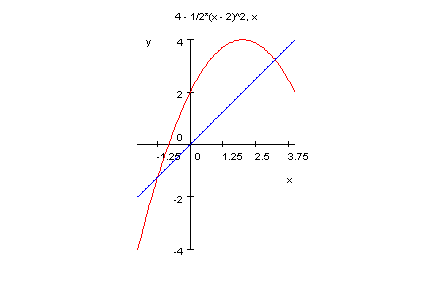

• fixgl:=f(x)=x

• assume(a>0):

• xfix:=solve(fixgl,x)

• op(xfix,1)   // Zugriff auf das 1. Element der Liste

• xfix1:=expand(%)  // besserer Term

• xfix2:=expand(op(xfix,2)) // Zugriff auf das 2. Element der Liste
  
  

• fixsteig1:=f'(xfix1); fixsteig2:=f'(xfix2) 

• fixsteig1:=expand(fixsteig1);fixsteig2:=expand(fixsteig2);

Für a= -1/8 ist die Wurzel Null, dann fallen beide Fixpunkte zusammen.
Dort ist die Steigung 1,

• a:=-1/8: plotfunc2d(f(x),x,x=-2..8, Scaling=Constrained);
  xfix;
  delete( a):
  

Ersichtlich ist bei xfix=6 ein anziehender Fixpunkt.
Weitere Untersuchung am rechten Fixpunkt:

• solve(fixsteig2=-1,a)  

• a:=3/8: plotfunc2d(f(x),x,x=-2..4, Scaling=Constrained);
  xfix;
  delete( a):

Also ist bei a=3/8 der rechte Fixpunkt xfix=10/3 anziehend,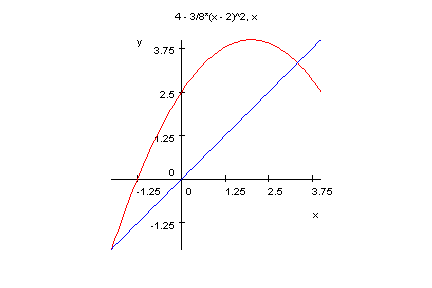
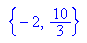
dort wird die Bifurkationskaskade eingeleitet.
Betrachtung der 2.Iterierten

• f2:=x->f(f(x));f2(x)

Die beiden neuen Fixpunkte der 2. Iterierten sind Häufungspunkte von f.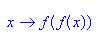
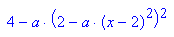
Sie sind zunächst anziehend. Die nächst Bifurkation findet statt, wenn in ihnen die
Steigung -1 wird. Die blaue Gerade zeigt Steigung -1, daher kommt es bei a=0.6 etwa hin.
Das passt auch zur Bifurkationskaskade aus Turboplot.

• a:=0.6:  plotfunc2d(f2(x),x,3-x,x=-1..5, Scaling=Constrained);
  delete( a):

Das Feigenbaumdiagramm (Attraktordiagramm) ist da zuende, wo die Folge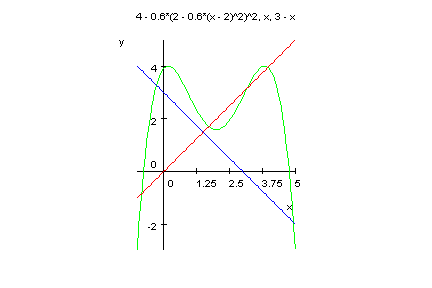
nach dem Maximum genau den Wert des linken Fixpunktes trifft.
In Turboplot scheint das für a=1 zu sein.
Probe:

• a:=1;f(f(2)); xfix1;delete a:

Also ist das richtig. Hätte man das auch herausbekommen?

• gl:=f(f(2))=xfix1;

• gl:=expand(2*a*gl)

• solve(gl,a)

Ja, da ist das Ergebnis konstruktiv erzeugt.
Damit reicht das Attraktordiagramm von a=-1/8 bis a=1.
Bifurkationen bei a=3/8 und etwa a=0,625 (erkundet in Turboplot).

© Prof. Dr. Dörte Haftendorn www.mathematik-verstehen.de	[Analysis]  [Computer] Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Apr 2003, update 15. August 2011	Site-Info Link zum Buch
	www.leuphana.de/matheomnibus       www.doerte-haftendorn.de https://mathe.web.leuphana.de     http://www.mathematik-sehen-und-verstehen.de