URLhaftendorn.uni-lueneburg.de/mathe-lehramt/kurven/hoehere/konchoiden/konchoiden.htm
[Kurven] [höhere Kurven] [Konchoiden] [Polarkoordinaten] 
|
URLhaftendorn.uni-lueneburg.de/mathe-lehramt/kurven/hoehere/konchoiden/konchoiden.htm |
|
[Kurven] [höhere Kurven] [Konchoiden] [Polarkoordinaten] |
| Entsprechend der allgemeinen Definition den Konchoiden ist speziell bei den Kreis-Konchoiden die "Straße", die Herrchen läuft, ein Kreis,der Baum steht irgendwo. Der Weg des Hundes -bei fester Leinenlänge k- ist eine Kreis-Konchoide. Für eine rechnerische Behandlung ist es am einfachsten, wenn der Baum im Ursprung steht. Steht der Baum auf dem Kreisrand, erhält man Pascalsche Schnecken 
|
| Herr Zvonimir Durcevic (Wien) (siehe auch Leitkreiskonstruktion der Kegelschnitte) nennt diese Kurven "Kreissehnen-Kurven". Er wird seine schöne systematische Übericht auch im Internet veröffentlichen. |
Schon 1998 haben die Kinder der 8. Klasse diese Formen entdeckt, siehe  |
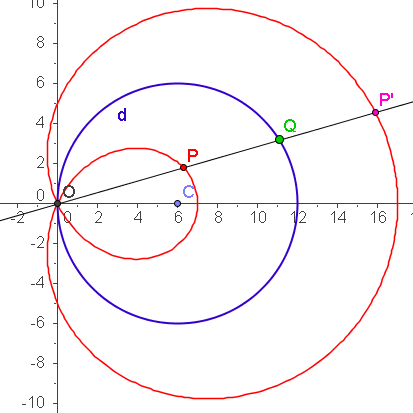
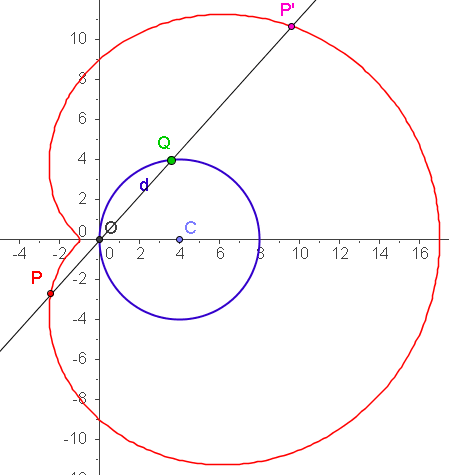
| Im Folgenden hat der Wanderkreis C seinen Mittelpunkt in (a,0) und den Radius c. Die Leinenlänge ist k. |
| Web MuPAD | MuPAD *mnb | Interaktiv  | download  |
|
| a>c | a4c3 |
a4c3 | Applet GeoGebra |
|
| a=c | a4c4 |
a4c4 | Applet GeoGebra |
|
| a<c | a4c5 |
a5c5 | Applet GeoGebra |
|
| a=6 c=7 k=5 | a=4 c=3.8 k=5 |
 |
 |
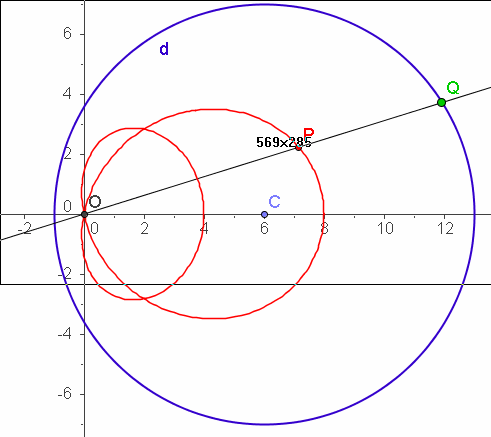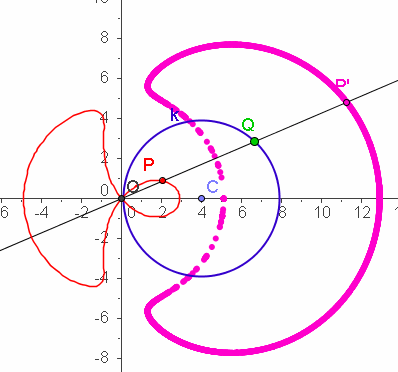| a=4 c=7 k=5 | a=4 c=9 k=8 |
 |
 |
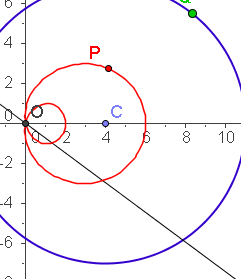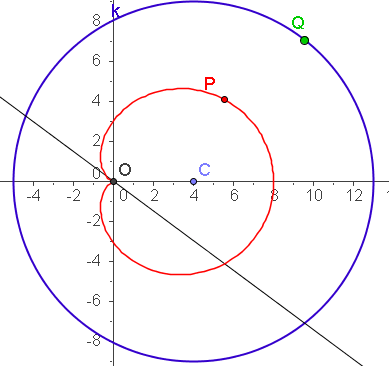| a=4 c=10 k=5 | a=4 c=5 k=5 |
 |
 |
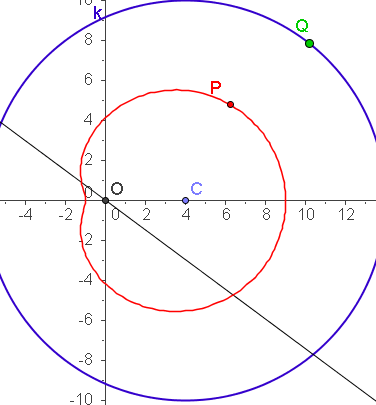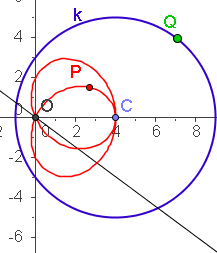es folgen Pascalsche Schnecken, siehe Extraseite | |
| a=4 c=4 k=5 | a=4 c=4 k=8 |
 |
 |
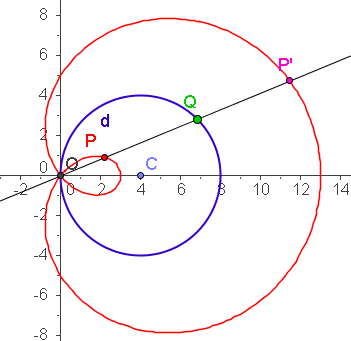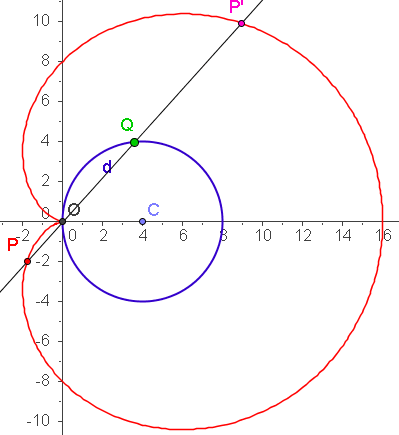| a=6 c=6 k=5 | a=4 c=4 k=9 |
 |
 |
|
[Polarkoordinaten]
[Kurven]
[Konchoiden]
[Höhere Geometrie]
[Inversion]
|
 Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn Juli 2005,, update |
| www.mathematik-verstehen.de www.doerte-haftendorn.de http://haftendorn.uni-lueneburg.de http://mathematik.uni-lueneburg.de |