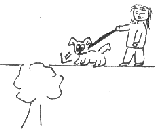
 Konchoide des Nikomedes:
Konchoide des Nikomedes: | Einführung geeignet ab Klasse 8 |
|
||||||||||||
| Gleichung ab Klasse 8 | Da in Klasse 8 weder Strahlensätze noch der Satz das Pythagoras verfügbar sind, ist eine Herleitung der Gleichung nicht möglich. Dennoch gehört ja das Bestimmen von Werten für einen Term und die die Verwendung eines x-y-Koordinatensystems zu den üblichen Lernzielen. Auf der Seite Terme und Gleichungen werden entsprechende Vorbereitungen mit passenden Arbeitsblättern vorgeschlagen. Wenn auf diese Weise der Boden bereitet ist, kann man die Gleichung der Hundekurve betrachten. Man sie hier abschreiben, aus dem Mathematikduden, aus dem Internet Famous Curves Index, England holen. 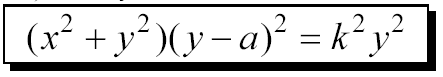 a ist der Abstand Straße-Baum, k ist die Leinenkänge Besonders spannend ist, y=a zu setzen und festzustellen, dass dazu kein x gehören kann. | ||||||||||||
| Zentrale Aussagen | Gleichungen mit x und y haben (fast immer) einen Graphen im x-y-System. Er wird von allen Punkten P=(x,y) gebildet, die beim Einsetzen die Gleichung zu einer wahren Aussage machen. Punkte P=(x,y), die beim Einsetzen die Gleichung zu einer falschen Aussage machen, gehören mit Sicherheit nicht zu dem Graphen der Gleichung. Ergibt sich nach einer Termumformung oder Gleichungsumformung ein anderer Graph, hat man mit Sicherheit falsch umgeformt. | ||||||||||||
| Übersicht mit Beweis ab der 9. Klasse |
Hundekurve= Konchoide des Nikomedes Erklärung, Beweis 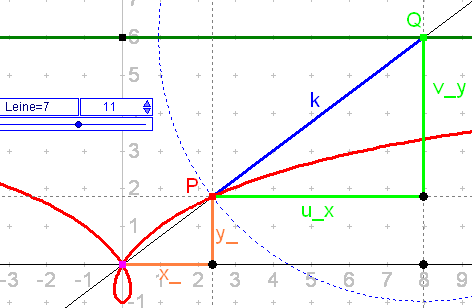 |
||||||||||||
| Hundekurve, Konstruktion, Geschichte, Gleichungen,... | |||||||||||||
Antike Problemlösung |
 Würfelverdoppelung mit der Konchoide Bild und Erklärung Würfelverdoppelung mit der Konchoide Bild und Erklärung |
||||||||||||
Ältere Dateien |
Konchoide (Joh) |
||||||||||||
| Konchoidenzirkel |
http://haftendorn.uni-lueneburg.de http://mathematik.uni-lueneburg.de |