Inversion der Strophoide

Leitseite zur Strophoide

Interaktiv mit GeoGebra

Strophoide, polar-kartesisch Inversion, mit minus-Zeichen

download

Strophoide, polar-kartesisch Inversion,mit plus-Zeichen

download

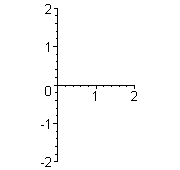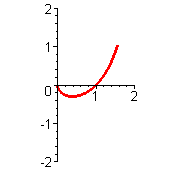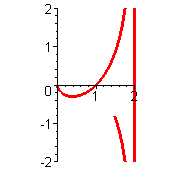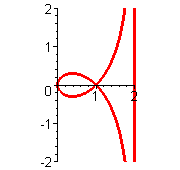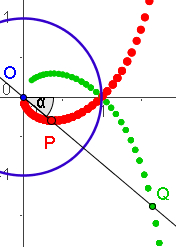
Die Strophoide ist eine analagmatische Kurve, d.h. sie kann bei Inversion in sich selbst übergehen.
Wie man sich an den oben gezeigten Graphen und Animationen überlegen kann, werden die beiden Kurven verschieden durchlaufen.
Polar-Formeln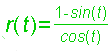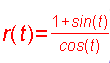

Weitere Erklärungen unten.
Geometrische Erzeugunsweisen der Strophoide finden Sie von der Leitseite Höhere Kurven aus.

Das "kann invertiert werden" (oben) bezieht sich darauf, dass Inversionskreis und Strophoide eine passende gegenseitige Lage haben müssen.
Soll der Inversionskries der Einheitskreis sein -was für die Übersichtlichkeit der Gleichungen wünschenswert ist-, muss die übliche Strophoidengleichung mit x->x-1 transformiert werden.
Herleitung der passenden Polarformeln

Diese Zeile ist der Beweis, dass die Strophoide in sich selbst übergeht.

Die Animationen sind mit Maple gemacht:
mit

Holt man weitere Graphikbefehele. Dann:

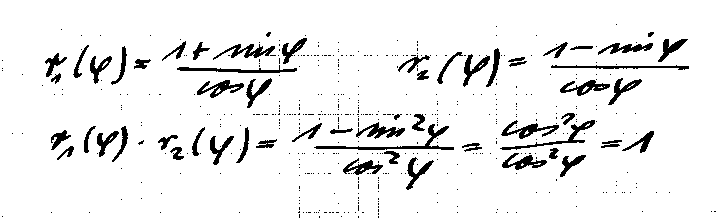
Es erscheint das Startbild und ein "Player". Man kann die Animation ansehen. Es immer nur ein Bild zu sehen. Markiert man das und wählt im "rechte-Maus-Menu" "Export als gif", so speichert man ein gif-Bild, das schon das animierte Bild ist.

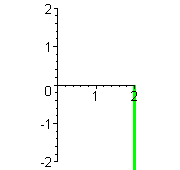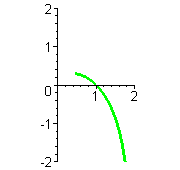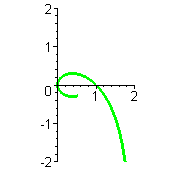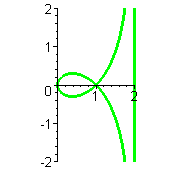
Wenn man sich klar machen will, wieso diese Durchlauf-Abfolge zustandekommt, ist es sinnvoll die Graphen der Terme mit t als Rechtsachse zu betrachten

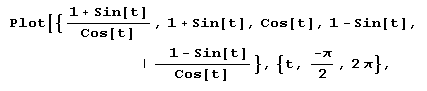
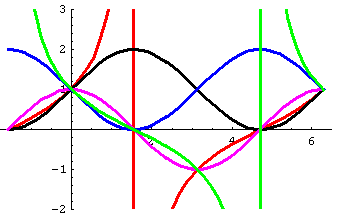Reihenfolge rot, schwarz, lila, blau, grün
Die beiden Polarradien sind rot und grün, wie oben.
Man sieht, dass sie stets gemeinsam positiv oder gemeinsam negativ sind.
Wo der eine 0 ist , hat der andere einem Pol.
Für 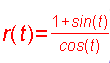ist die Nullstelle bei Pi/2 leicht durch die l'Hospitalsche Regel zu gewinnen.
Das gilt ebenso für die Nullestelle 3Pi/2 von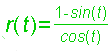
1 und -1 nehmen sie gemeinsam an.

[Computer] [Kurven] [Geometrie] [Höhere Geometrie] [Inversion]

Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn Frühjahr 1998, update 13. Juni 2012

www.mathematik-verstehen.de www.doerte-haftendorn.de
https://mathe.web.leuphana.de http://mathematik.uni-lueneburg.de