www.mathematik-verstehen.de
mathe.web-leuphana.de/algebra/algebra.htm
[Algebra] [Aufbau des Zahlsystems] [Analysis [Cardano] [Geschichte] [MuPAD] [GeoGebra] [Didaktik]
Komplexe Zahlen und FunktionenDie Erweiterung von den reellen Zahlen zu den komplexen  ordnet sich bei den
algebraischen Erweiterungen ein und ist auf der Seite "Aufbau des Zahlsystems" beschrieben. Die wesentlichen Definitionen stehen aber auch auf dieser Seite bei "Rechnen".
|
 |
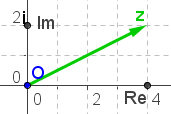
| Darstellung | In der Gaußschen Zahlenebene haben die komplexen Zahlen die Gestalt .Dabei heißt a der Realteil von z, Re(z) und b der Imaginärteil von z Im(z). Der reelle Zahlenstrahl heißt nun "reelle Achse", die senkrechte Achse enthält alle reelle Zahlen versehen mit dem Faktor i, wobei  ist. |
 |
|
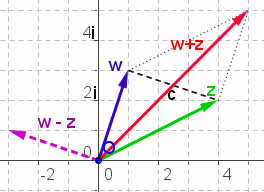
| Strichrechnung | Die Addition erfolgt in der Gaußschen Zahlenebene entsprechend der Vektoraddition, ebenso die Subtraktion |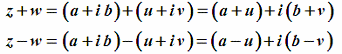
 |
|
| Multiplikation | Die Multiplikation ist algebraisch passend definiert:
Visualisierung:  Komplexe Zahlen, Summe und Produkt  |
||
| Division | 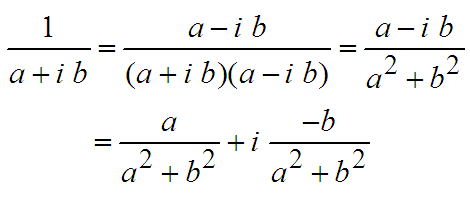 Diese Umrechnung ist wichtig, damit auch das Inverse die üblich Darstellung x+i y bekommt. Ein tieferes Verständnis des Inversen gewinnt man erst mit der Polardarstellung und der Inversion am Kreis.
( , +,*) ist ein vollständigiger Körper, der sich aber nicht anordnen lässt. |
||
| Darstellung |  |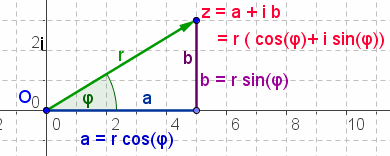
||
| Taylorreihen | 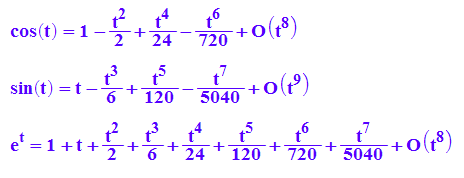 Sieht man sich die Taylorreihen von cos, sin und e an, dann erkennt man die strukturelle Gleichheit. Die e-Funktion ergibt sich nicht als Summe, da stimmen die Vorzeichen nicht. Nimmt man aber nicht t als Argument der e-Funktion sondern it, so passt es: |
||
| Eulersche Formel Polardarstellung |
Also gilt die Eulersche Formel 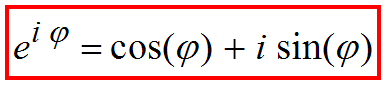 und für komplexe Zahlen gilt die Polardarstellung: 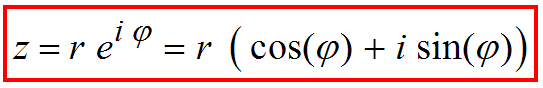 r heißt Betrag von z und phi heißt Argument von z, oder (Argument)-Winkel von z |
||
| Multiplikation |  Quadrat bilden: Winkel verdoppeln, Betrag quadrieren  Produkt bilden: Beträge multipizieren, Winkel addieren Visualisierung des Produktes
Geometrische Erzeugung des Produktes
|
||
| TI nspire |
 Komplexe Zaheln mit TI Handzettel download  | ||
| Division | 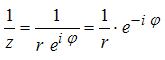 Inverses bilden: Kehrwert des Betrages und Negatives des Winkels nehmen: 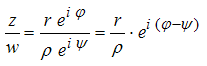 Quotient bilden: Quotient der Beträge und Differenz der Winkel nehmen: Geometrische Erzeugung des Inversen mit Stahlensatz Komplexe Zahlen, Inverses geometrisch mit Strahlensatz Geometrische Erzeugung des Inversen mit Inversion am Kreis Komplexe Zahlen, Inverses geometrisch mit Inversion am Kreis Weiteres zur Inversion |
||
|
[Algebra]
[Aufbau des Zahlsystems]
[Analysis
[Geschichte]
[Riemann]
[MuPAD]
[GeoGebra]
[Didaktik]
| |||
 Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn Nov 2006, update | |||
|
