www.mathematik-verstehen.de
[Komplexe Zahlen] [Algebra] [Aufbau des Zahlsystems] [Analysis [Cardano] [Geschichte] [MuPAD] [GeoGebra] [Didaktik]
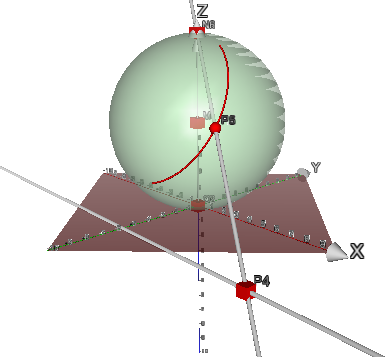 |
Die Riemannsche Zahlenkugel hat den Radius 1, den Südpol im Ursprung und den Nordpol in N=(0,0,1). N gehört nicht zur Riemann-Kugel Jeder Punkt P der Gaußschen Zahlenebene wird auf den Durchstoßpunkt Geraden PN durch die Kugel abgebildet. Die Abbildung der Gaußschen Zahlenebene auf die Riemann-Kugel ist bijektiv. Sehr ferne Punkte werden auf Punkte in der Nähe der Nordpols abegebildet. |
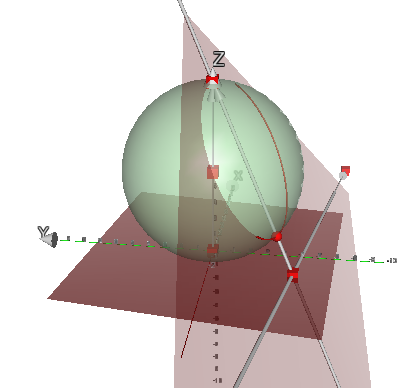 | Es gibt genau eine Ebene durch eine Gerade in der Gaußschen Zahleneebene und den Nordpol der Riemann-Kugel. Diese schneidet die Kugel in einem Kreis durch den Nordpol. Alle Punkte dieses Kreises außer dem Nordpol selbst sind Bilder von Geradenpunkten und umgekehrt.
|
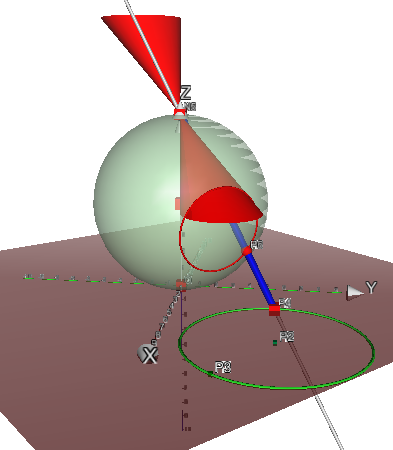 Kreise der Gaußschen Zahlenebene werden auf Kreise auf der Riemannkugel abgebildet, die keine Lücke beim Nordpol haben und umgekehrt. Kreise der Gaußschen Zahlenebene werden auf Kreise auf der Riemannkugel abgebildet, die keine Lücke beim Nordpol haben und umgekehrt.
|
|
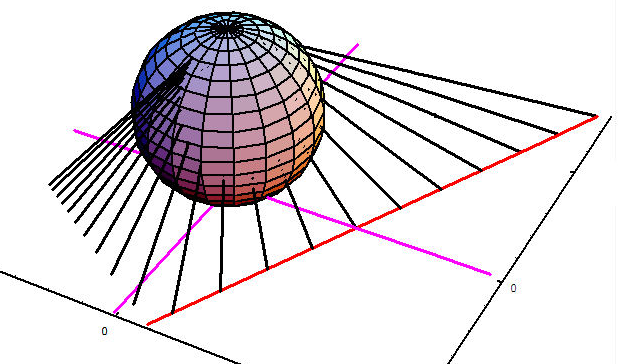 |
|
|