[Algebra] [Analysis [Cardano] [Geschichte] [MuPAD] [GeoGebra] [Didaktik]
| www.mathematik-verstehen.de | |||
[Algebra] [Analysis [Cardano] [Geschichte] [MuPAD] [GeoGebra] [Didaktik] | |||
ZahlbereichserweiterungenAuf dieser Seite sollen einige tragende Gedanken aller Zahlbereichserweitungen betrachtet werden. Schwerpunkt liegt zunächst auf den algebraischen Erweiterungen. Der Übergang von den rationalen |
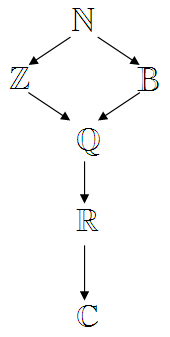 |
| Definition | Äquvalenzrelation Anwendung auf das Modulo-Rechnen und Kryptografie |
| Paarbildung | Jedes Paar P=(a,b) lässt sich im Koordinatensystem darstellen. |
| Äquivalenz | a,b) äq (x,y) genau dann wenn a y = b x Zu (a,b) sind alle Paare (x,y) äquivanent, die auf der Ursprungsgeraden a y=b x liegen, also der Geraden y=b/a x (nur Gitterpunkte im 1. Quadranten!) Dieses entspricht der Gleichheit von Brüchen, die durch Erweitern oder Kürzen auseinander hervorgehen können. (a,b) äq (x,y) genau dann wenn a+y = b + x Zu (a,b) sind alle Paare (x,y) äquivalent, die auf der Geraden y+a=x+b mit Steigung 1 durch (a,b) liegen, also der Geraden y=(x-a) +b (nur Gitterpunkte im 1. Quadranten!)Für die Vorstellung "differenzengleiche Zahlenpaare" (a,b) äq (x,y) genau dann wenn a+y = b + x Zu (a,b) sind alle Paare (x,y) äquivalent, die auf der Geraden y+a=x+b mit Steigung 1 durch (a,b) liegen, also der Geraden y=(x-a) +b (nur rationale nichtnegative Koordinaten!) (a,b) äq (x,y) genau dann wenn a y = b x Zu (a,b) sind alle Paare (x,y) äquivanent, die auf der Ursprungsgeraden a y=b x liegen, also der Geraden y=b/a x (nur Gitterpunkte aller Quadranten!) |
| Definition der Summe |
(a,b)+(c,d):=(a d + b c , b d), dies entspricht der Summe von Brüchen. Dies ist erlaubter Punkt, also ist die Abgeschlossenheit der Addition gesichert. Zu zeigen bleibt die Repräsentantenunabhängigkeit. Das heißt: Nimmt man statt (a,b) einen anderen erlaubten Punkt der Ursprungsgeraden durch (a,b) und nimmt man statt (c,d) einen anderen erlaubten Punkt der Ursprungsgeraden durch (c,d), so ergibt sich als Summe ein anderer erlaubter Punkt der Ursprungsgeraden durch (a d + b c , b d). Visualisierung: Die "falsche Summe" zeigt, dass die falsche Regel "...Zähler+Zähler, Nenner+Nenner" nicht Repräsentantenunabhängig ist. Setze dazu Spur auf FS. Formaler Beweis 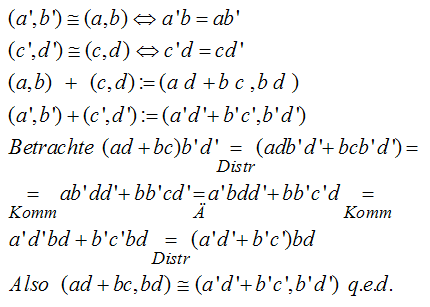 Von diesem Kaliber sind alle Beweise, die in diesem Thema bei formal-strengem Vorgehen notwendig sind. Hinzu kommt noch die Betrachtung von Sonderfällen, die die 0 an der rechten Stelle des Paares betreffen, also eigentlich dazu dienen, die Division durch 0 vermeiden. Grundprinzip aller dieser Beweise ist der Rückgriff auf die Gesetze, die in dem Ausgangs-Zahlbereich schon gelten. Ziel aller Definitionen ist die "Rettung" aller dieser Gesetze, sie sollen in dem zu konstruierenden Zahlbereich weiter gelten und der ursprüngliche Zahlbereich soll eingebettet werden. Damit man etwas Handwerk lernt, sind hier die Durchführungen der Mal-Erweitung für die beiden Übergamge Natürliche Zahlen zu Bruchzahlen, und Ganze Zahlen zu Rationale Zahlen. Es ist mit dem Durchhalten aller Beweise kein weiterer Erkenntnisgewinn verbunden. Das geht jetzt nach dem Motto "..... wir denken uns die Dose offen" mehr zu dem Witz mit der Dose.. (a,b)+(c,d):= (a+c,b+d). Dieses entspricht der Vektordefinition. Dies ist erlaubter Punkt, also ist die Abgeschlossenheit der Addition gesichert. Zu zeigen bleibt die Repräsentantenunabhängigkeit. Das heißt: Nimmt man statt (a,b) einen anderen erlaubten Punkt der Geraden durch (a,b) mit Steigung 1 und nimmt man statt (c,d) einen anderen erlaubten Punkt der Geraden durch (c,d) mit Steigung 1 so ergibt sich als Summe ein anderer erlaubter Punkt der Geraden durch (a+c,b+d) mit Steigung 1. Visualisierung: (a,b)+(c,d):= (a+c,b+d). Dieses entspricht der Vektordefinition. Dies ist erlaubter Punkt, also ist die Abgeschlossenheit der Addition gesichert. Die Repräsentantenunabhängigkeit braucht nicht gezeigt zu werden, denn man bildet gar keine Äquivalenzklassen. |
| Definition des Produktes |
(a,b)*(c,d):=(a * c , b* d), dies entspricht dem Produkt von Brüchen. Dies ist erlaubter Punkt, also ist die Abgeschlossenheit der Addition gesichert. Zu zeigen bleibt die Repräsentantenunabhängigkeit. Das heißt: Nimmt man statt (a,b) einen anderen erlaubten Punkt der Ursprungsgeraden durch (a,b) und nimmt man statt (c,d) einen anderen erlaubten Punkt der Ursprungsgeraden durch (c,d), so ergibt sich als Summe ein anderer erlaubter Punkt der Ursprungsgeraden durch (a * c , b *d). Visualisierung: (a,b)*(c,d):= (a c + b d,a d + b c). Dies findet man aus (a-b)(c-d). Dies ist erlaubter Punkt, also ist die Abgeschlossenheit der Addition gesichert. Zu zeigen bleibt die Repräsentantenunabhängigkeit. Das heißt: Nimmt man statt (a,b) einen anderen erlaubten Punkt der Geraden durch (a,b) mit Steigung 1 und nimmt man statt (c,d) einen anderen erlaubten Punkt der Geraden durch (c,d) mit Steigung 1 so ergibt sich als Summe ein anderer erlaubter Punkt der Geraden durch (a+c,b+d) mit Steigung 1. Visualisierung: Von (a,b)*(c,d):= (a c - b d, a d + b c). Dies findet man aus (a+ib)(c+id). Dies ist erlaubter Punkt, also ist die Abgeschlossenheit der Addition gesichert. Die Repräsentantenunabhängigkeit braucht nicht gezeigt zu werden, denn man bildet gar keine Äquivalenzklassen. Visualisierung: Geometrische Erzeugung des Produktes Geometrische Erzeugung des Inversen mit Inversion am Kreis Geometrische Erzeugung des Inversen mit Stahlensatz |
| Algebraische Stukturen |
Die Axiome für Halbgruppen, Gruppen, Halbringen, Ringen und Körpern sind auf den Seiten "Gruppenbegriff" Regularität: aus a+d=c+d folgt a=c b.z.w. aus a d = c d folgt a=c. Gruppen sind sowieso regulär. In Halbringen, Ringen und Körpern gilt das Distributivgesetz von * über + , also a*(b+c)=a*b+a*c. Er ist regulär bzl. + und * und besitzt eine Totalordnung, das heißt es gibt den Zahlenstrahl [0,unendlich) mit 0,1,2,3,4,5.... ( Er ist regulär bzl. + (und *) und besitzt eine Totalordnung. ( Der Zahlenstahl [0,unendlich) ist dicht, d.h. zwischen je zwei Bruchzahlen gibt es stets eine weitere Bruchzahl, d.h. man kann die Bruchzahlen zwar ordnen, aber nicht der Größe nach notieren. ( das bedeutet ( Er ist regulär bzl.( + und) * und besitzt eine Totalordnung, das heißt es gibt den Zahlenstrahl (-unendlich,unendlich) mit ....-5,-4,-3,-2,-1,0,1,2,3,4,5.... ( das bedeutet ( ( Er ist dicht, d.h. zwischen je zwei Bruchzahlen gibt es stets eine weitere Bruchzahl, d.h. man kann die Bruchzahlen zwar ordnen, aber in keinem Intervall der Größe nach notieren. In ( |
| Einbettung und Darstellung |
Grundsätzlich werden äquivalente Zahlenpaare zu Klassen zusammengefasst und die Klassen sind dann die Objekte, für die man die oben genannten algebraischen Eigenschaften beweist. 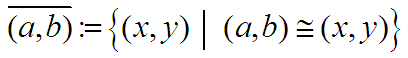 . . Eine solche Konstruktion von Objekten neuer Art nennt man "Reifikation" (sprich re-ifikation). Nun bleibt zweierlei zu tun:
Für die Einbettung braucht man eine Abbildung 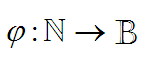 mit mit 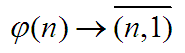 , die "strukturverträglich ist: , die "strukturverträglich ist:
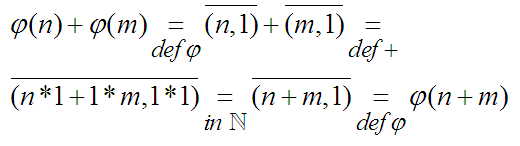
"Die Summe der Bilder ist gleich dem Bild der Summe." ebenso ist zu zeigen: "Das Produkt der Bilder ist gleich dem Bild des Produktes." Eine solche strukturverträgliche Abbildungen heißt ganz allgemein "Homomorphismus". Ist die Abbildung zusätzlich eine Bijektion (eineindeutig auf...) heißt sie "Isomorphismus". Zur Darstellung definiert man: 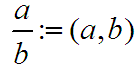 . Zum Glück hat man alles so eingerichtet, dass das ganze "Gesetzeswerk" von oben nun die normale Bruchrechnung ergibt, wie man sie sich an Torten, Pizza und Schokolade klarmachen kann. Hier reift auch die Erkenntnis, dass der Weg über die Zahlenpaare schulisch völlig unbrauchbar ist.
Das Bruchsymbol bewahrt ja wenigstens noch die Paarbildung und äquivalente Paare sind Brüche, die durch Kürzen und Erweitern auseinander hervorgehen können. . Zum Glück hat man alles so eingerichtet, dass das ganze "Gesetzeswerk" von oben nun die normale Bruchrechnung ergibt, wie man sie sich an Torten, Pizza und Schokolade klarmachen kann. Hier reift auch die Erkenntnis, dass der Weg über die Zahlenpaare schulisch völlig unbrauchbar ist.
Das Bruchsymbol bewahrt ja wenigstens noch die Paarbildung und äquivalente Paare sind Brüche, die durch Kürzen und Erweitern auseinander hervorgehen können.Man nun auch sagen: Die Natürlichen Zahlen mit plus und mal sind isomorph zu den Brüchen mit Nenner 1 mit plus und mal der Bruchrechnung. Übrigens: Schüler trauen sich oft nicht, die 1 im Nenner wegzulassen! Da steckt ja eine tiefe Wahrheit drin! Für die Einbettung braucht man eine Abbildung Für die Darstellung muss man sich fachwissenschaftlich etwas mehr anstrengen, da die Paarbildung in der übelichen Schreibweise nicht erhalten bleibt. Man muss klären, dass es nur drei Klassentypen gibt Äquivalente Zahlenpaare sind solche mit "gleicher Differenz", also (5,12) äq (18,9)äq.... äq (0,7). Während in der Schule 5-12 bzw. k-z allgemein überhaupt keine Probleme macht, gehört zur strengen Fachwissenschaft hier Für Lehrer interessant ist allerdings, dass der Ausdruck 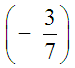 aus der Erwiterung von Z nach Q stammt, während aus der Erwiterung von Z nach Q stammt, während In der reellen Achse kann man das eingebette R direkt sehen. Die Darstellung in der Form Beachte hierzu auch 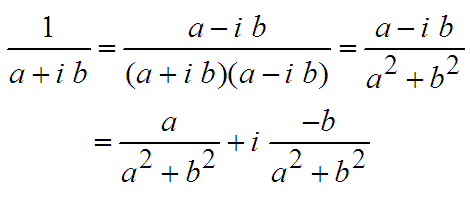
Siehe auch extra Leitseite Komplexe Zahlen und Funktionen |
https://mathe.web.leuphana.de |