www.mathematik-verstehen.de
https://mathe.web.leuphana.de/geschichte/riemann/riemann.htm[Analysis] [Integrale] [Reihen] [Geschichte der Mathematik]
Bernhard Riemann,
|
|
|
|
||
Bernhard Riemanns Kindheit und Schulzeit am Johanneum zu Lüneburg |
|
| Frühe Kindheit | Lüneburg liegt 70 km südöstlich von Hamburg. Website der alten Salzstadt Lüneburg |
| Das Hannoversche Wendland ist auch heute noch ein dünn besiedelter Landstrich, der die wendische Siedlungsform des Rundlings lange bewahrt hat. In einem solchen sehr kleinen Dorf, Breselenz am Rand des Höhenzuges Drawehn, kam Bernhard Riemann am 17. September 1826 als das zweite von sechs Kindern des Pastors zur Welt.
Sein Elternhaus wurde vor seinem Abbruch in einer Fotografie festgehalten.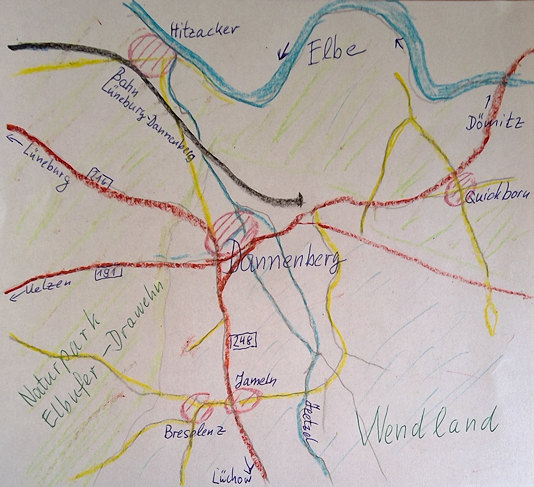   
In früher Kindheit brachte er den seine Kinder unterrichtenden Vater und später einen extra für Mathematik engagierten Hauslehrer an die Grenzen ihres Verständnisses. [GA Ded]. Obwohl der Vater inzwischen ein Pfarre in Quickborn in unmittelbarer Nähe des Städtchens Dannenberg innehatte, war eine höhere Schulbildung auch dort nicht möglich. Ein Gymnasium ist in Dannenberg erst in den 1970-iger Jahren entstanden. Zu Riemanns Jugendzeit in der Elbmarsch und in Lüneburg haben A. und D. Laugwitz [Lau] einen bebilderten Artikel auf Englisch verfasst.   Wohnhaus und Kirche in Quickborn, heute Dannenberg Nach seiner Konfirmation Ostern 1840 wurde der begabte Junge zu seiner Großmutter, einer Hofratswitwe, nach Hannover geschickt, damit er dort die Tertia des Lyceums besuchen konnte. Dedekind [GA Ded], der die Korrespondenz mit der Familie ausgewertet hat, berichtet von besonderes innigen familiären Bindungen. Der Anschluss an fremde Menschen fällt dem jungen wie später auch dem älteren Riemann schwer. In unserem Zusammenhang ist interessant, dass sein Mathematiklehrer zunächst verstimmt ist, dass der Schüler ihn fachlich berichtigen konnte, dann aber sein Können akzeptieren lernt und ihm "ein besonderer Freund" wird, wie Schering in seiner Gedächtnisrede erwähnt. [GA Scher]. Schering schätzt es als günstige Fügung ein, dass Riemann nach dem Tod der Großmutter an das Johanneum in Lüneburg wechselt. | |
| Schulzeit am Johanneum |   Johanneum Bau von 1829, Direktor Dr. Carl Haage |
Das Johanneum befand sich gerade eine Phase des Aufstiegs. Bis in das 19.Jhdt hinein gab es eigentlich den Lehrberuf nicht. Alle Fächer wurden von Theologen unterrichtet, die oft baldmöglichst eine Pfarre annahmen. Diesem Übel abzuhelfen wurde 1823 der junge und überaus tüchtige Dr. Carl Haage aus Gotha berufen. Dank seines engagierten Wirkens blühte die Schule auf. Er initiierte auch ein neues Gebäude, da das alte "zu eng und dumpf geworden" und keinen Raum bot "für ein Naturalien - und physikalisches Kabinett, wie es auf Dauer nicht zu entbehren sei." In Haages Zeit fiel 1829 die Neuorganisation des gesamten hannoverschen Schulwesens mit Einführung einer Schulbehörde und von Maturitätsprüfungen. "Es wurde ihm (Haage) die 'außerordentliche Freude und Genugtuung', dass die Arbeiten der Abiturienten des Johanneums bei der ersten Maturitätsprüfung die besten waren und dass bei der ersten Visitation der Schulrat Kohlrausch erklärte, 'dass das Johanneum nicht nur die beste Schule im Hannoverschen sei, sondern auch unter den dreißig Schulanstalten, die er in seinem vorherigen Wirkungskreise als preußischer Schulrat kennengelernt habe'. Die Anerkennung Haages reichte so weit, dass "ihn die Georgia Augusta zu Göttingen bei ihrer Jubelfeier 1837 zum Ehrendoktor ernannte".
Eigene Seite zu Carl Haage 
 Insbesondere hatte der Unterricht in Mathematik unter der alleinigen Herrschaft der Theologen und Philologen zu leiden gehabt bis Haage 1829 den ersten -und auf lange Zeit einzigen- studierten Mathematiker, Constantin Schmalfuß einstellte,"...der in seltener Weise strenge mathematische Schulung und Gedankenzucht mit Geschmack und ästhetischer Bildung verband und seinem Lehrfach mit einem Schlage die gebührende Stellung im Ganzen des Lehrplans und, was nicht zu unterschätzen ist, auch in der Wertung der Schüler eroberte."
Auch Schmalfuß stammte aus Thüringen und hatte in Halle und Berlin Mathematik studiert. Er war unter Haage Konrektor und übernahm nach dessen plötzlichen Tod im Dez. 1842 die Amtsgeschäfte. "Er war ein hervorragender Lehrer und ausgezeichneter Verwaltungsmann" und "hat es in den 6 Jahren seiner Amtsführung aufs Beste verstanden, das Ansehen des Johanneums zu wahren und die Bedenken 'ob ein Mathematiker für diesen Posten wohl recht geeignet sei' gründlich zu zerstören." Im Königreich Hannover "stand dieser Vorgang ohne Beispiel da." Eigene Seite zu Constantin Schmalfuß Im Hinblick auf Bernhard Riemanns Biographie ist es ausgesprochen bemerkenswert, dass auch in den nachfolgenden 150 Jahren nie wieder ein Mathematiker oder Naturwissenschaftler Direktor des Johanneums war. Bis auf den Sohn des oben erwähnten Schulrats, der wenigstens Mathematik als Zweitfach hatte, hat es zwischen 1849 und 1867 keinen Mathematiker als Lehrer gegeben. Bernhard Riemann trat Ostern 1842 in die Untersekunda (heute 10. Klasse) des Johanneums ein. Zu diesem Zeitpunkt besuchten 281 Schüler die Schule.  großes Bild In der Festschrift von 1906 ist der Lehrplan abgedruckt, der bei Riemanns Eintritt in Johanneum galt. Riemann sollte nach den Vorstellungen seines Vaters Pastor werden und besuchte daher nicht "Realklassen" mit stärkerer Betonung der Mathematik, des technischen Zeichnens, der neuen Sprachen und der "Naturgeschichte". Außerdem brauchte man damals für eine wissenschaftliche Laufbahn unumgänglich gute Lateinkenntnisse. Da er ohnehin Schmalfuß als Mathematiklehrer hatte und sowieso schneller begriff als seine Mitschüler, gereichte ihm das nicht zum Nachteil. | |
| Mathematik bei Schmalfuß |
Von Schmalfuß' Beziehung zu Bernhard Riemann wissen wir vor allem durch den Brief, den Schering vor der Verfertigung eines Nachrufes nach Riemanns Tod 1866 von Schmalfuß erhalten hat [GA /851ff]. Er schreibt dort: "...Die Fassungskraft für mathematische Gegenstände gab sich mir sofort kund und es bedurfte bei Riemann nur der Andeutung eines mathematischen Gesetzes, um dasselbe mit den weitesten Consequenzen in feste Form gebracht zu sehen, und zwar in größter Allgemeinheit."
.... Alles was ich besitze an Euklidischen Dingen, mit den Kommentaren ...; was ich von der Archimedischen Literatur besaß, Apollonios etc. alles dies las er, und unter dem Lesen ward es sein sicheres Eigenthum. Newtons Arithmetica universalis und des Cartesius Geometria interessierten ihn nicht minder. ..." Schmalfuß läßt ihn zwar am normalen Mathematikunterricht teilnehmen, aber "....vielmehr sann ich darauf, ihm in jeder Stunde etwas zu bieten, was seinen Kräften angemessen war, und jedesmal ist er über die Grenze, die ich als seine Schranke und wohl auch als meine betrachtete, hinausgegangen und brachte regelmäßig eine Fülle von Ergebnissen, die ich nicht in solchem Maße erwartet hatte." Laugwitz [Lau] gibt zu Bedenken, dass, nachdem nun der Schüler berühmt geworden ist, möglicherweise zu "rosig" aus seiner Schulzeit berichtet wird. Es passt aber zu der von dem Altphilologen Nebe [FS Neb] ausführlich geschilderten Persönlichkeit Constantin Schmalfuß', dass er sich in Riemanns Situation und Persönlichkeit schon zur Schülerzeit eingefühlt hat und auch entsprechend tatkräftig gehandelt hat (s.u.). Es ist bei Nebe die Rede von "seiner feinen und gewandten, offenen und heiteren Art sich zu geben,...sicheren Geschäftsgewandtheit bei idealster Auffassung des Lehrerberufes,...weiches, ungemein wohlklingendes Organ,....Sachkenntnis und rasche Auffassung,..." So kann man es wohl ernst nehmen, wenn Schmalfuß schreibt: "...daß ich Riemann mehr verdanke, als er mir" "... ich bedaure sehr, daß mir nichts geblieben ist, von der Sinnigkeit und Einfachheit seiner Beweisführungen und Formelentwicklungen. Schon damals war er ein Mathematiker, neben dessen Vermögen der Lehrer sich arm fühlte...." Am Schluß schreibt Schmalfuß: "Ich für meinen Theil habe es immer für ein großes Glück angesehen, daß ich einen solchen Schüler, wie Riemann, gehabt habe, und bin ihm heute noch für die vielfache Anregung, die er mir gegeben hat, und für die Freude, die ich an seiner wunderbaren Begabung und Entwickelung gehabt habe, für meine ganze Lebenszeit dankbar." Mehr aus dem Brief von Schmalfuß
|
| Wohnen bei Seffer |
Ein weiterer Lehrer Riemanns, der Religions- und Hebräischlehrer Dr. Gustav Heinrich Seffer, hat sich Schering gegenüber in einem Brief vom Nov. 1866 geäußert.[GA /849] Er war erst 25 Jahre alt, als Riemann ans Johanneum kam. Mit dem zehn Jahre älteren Schmalfuß verband ihn eine Freundschaft. Die beiden versuchten mit vereinten Kräften, ein großes Problem des begabten Schülers zu lösen. Schmalfuß schreibt von Riemann: "... wie schwer es ihm wurde, in fließendem Vortrage seine Gedanken zu entwickeln. Dazu kam, daß kein Ausdruck ihm genügte, der nicht alles umfaßte, und daß er ungemein zaghaft war, eine Darstellung, die nicht, ... , von untadeliger Präcision war, als richtig anzuerkennen. ...." Seffer sagt: ".... daß er mit seinen deutschen und lateinischen Aufsätzen immer im Rückstande blieb,..., daß die Lehrer-Conferenz den Schulgesetzen gegenüber seinetwegen in Verzweiflung war." Mit heutigem Vokabular hieße das, Bernhard Riemann erfüllte nicht die Plichtauflagen. Da die beiden nicht tatenlos ansehen wollten, wie sein Abitur aus "formalen Gründen" in Gefahr geriet, nennt Seffer die Lösung: "...nahm ich ihn gegen ein ermäßigtes Kostgeld in mein Haus und verpflichtete mich gegen die Lehrer-Conferenz für prompte Ablieferung seiner Aufsätze von nun an sorgen zu wollen. .... und habe manchen Abend bis in die Nacht bei ihm gesessen...."
Laugwitz meint angesichts Seffers Wohnhaus an Riemanns Qualen denken zu müssen, sich als ein an Leib uns Seele Gefangener zu sehen...[Lau]. Für diese Auffassung habe ich keinerlei Anhaltspunkte gefunden. Im Gegenteil erscheint Seffer eher wie ein großer Bruder, dessen Beharrlichkeit und Kompetenz helfen, dass Bernhard Riemann letztlich lernt, eine schriftliche Arbeit zuendezuführen. Seffer verfasste zu derselben Zeit ein "Elementarbuch der hebräischen Sprache, das jetzt auf den Gymnasien Deutschlands und der Schweiz viel gebraucht wird." Das Werk sollte zu allen Kapiteln genau passende Übungsstücke enthalten. Diese aus der Bibel herauszusuchen, "war eine schwierige Aufgabe, für die sich Riemann lebhaft interessierte. ....daß mein Elementarbuch mehrere seiner Übungsstücke zum großen Theil dem großen Mathematiker Riemann zu verdanken hat." Riemann hat Seffer Jahre später noch besucht, was besser zu einem Gefühl der Dankbarkeit und wenig zu dem des Hasses passt, und der Lehrer schreibt davon: "später... hat er mir viel von seiner philosophischen Arbeit erzählt. .... Ich muß freilich gestehen, daß ich ihm keineswegs folgen konnte,...., aber doch die Großartigkeit seiner Ziele bewundern mußte." Er schließt seinen Brief " Riemann war still, bescheiden und anspruchslos,..... namentlich im Verkehr mit Damen leicht verlegen....Ich habe ihn immer liebgehabt und behalten." Mehr aus dem Brief von Seffer
|
| Abitur | 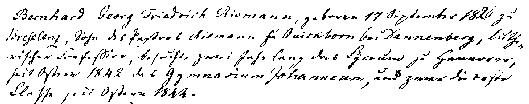 Maturitäts-Zeugniß erster Klasse großes BildBernhard Georg Friedrich Riemann, geboren 17. September 1826 zu Breselenz, Sohn des Pastors Riemann zu Quickborn bei Dannenberg, lutherischer Konfession, besuchte zwei Jahre lang das Lyzeum zu Hannover, seit Ostern 1842 das Gymnasium Johanneum, und zwar die erste Klasse seit Ostern 1844. Also besuchte er Unter- und Odersekunda und Unter- und Oberprima, in heutiger Bennennung 10. bis 13. Klasse. |
|
Es war abzusehen -und trat dann auch wirklich ein-, dass Riemann den Abituraufsatz in der gegebenen Zeit nicht vollenden würde. Schmalfuß aber wollte Riemann dennoch ein Zeugnis "erster Klasse" ermöglichen. Nun war ihm als einzigem Mathematiker klar, dass es schwer sein würde, die Altphilologen und Theologen von Riemanns mathematisch überragenden Können zu überzeugen. Er ersann folgende völlig legitime List: Bernhard hatte zu Pfingsten des Vorjahres für eine Woche Legendres Zahlentheorie ausgeliehen gehabt. Als er es so schnell zurückgab, mutmaßte der Lehrer, es sei wohl zu schwierig gewesen. Riemann hatte das verneint, das Buch interessant gefunden und ganz gelesen. Schmalfuß beschloß nun, ihn genau das ohne Ankündigung zu prüfen, dann müsse ja auch jeder mathematische Laie sehen, dass es sich um eine ganz ungewöhnliche Leistung handele. Er prüft ihn deshalb über die weit über den Schulunterricht hinausgehende Zahlentheorie von Legendre und stellt dann fest:.. "daß ihm alles, worauf ich als Examinator mich nicht ohne Mühe vorbereitet hatte, ..., geläufig war". So kam es tatsächlich zum Maturitätszeugnis "erster Klasse".
Speziell zur Mathematik heißt es im Zeugnis [Abi]: Mathematik. Seine Kenntnisse sind durchaus gründlich und sicher und gehen an Umfang und Tiefe weit über das Maß hinaus, das der Mathematik an Schulen eingeräumt werden kann, in Auffaßung mathematischer Lehren besitzt er Scharfblick, Raschheit und Klarheit in seltenem Grade. Er wird unterstützt durch ein zuverlässiges Gedächtniß, eine ausgezeichnete Kombinationsgabe und Behendigkeit einer konstruierenden Phantasie. 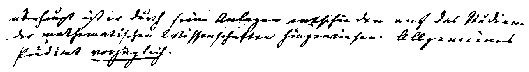 Originalteil in Sütterlinschrift, in Druckschrift: Überhaupt ist er durch seine Anlagen entschieden auf das Studium der mathematischen Wissenschaften hingewiesen. Allgemeines Prädikat vorzüglich.   Nach sorgfältiger Prüfung und Berathung ist dieses Zeugniß erster Klasse nach gewissenhafter Überzeugung beschlossen und ausgefertigt von der Prüfungskommission des Gymnasiums Johanneum zu Lüneburg den 10ten März 1846 Schmalfuß Im Hinblick darauf, dass aber allenthalben die Gründlichkeit, Prägnanz und Eigenständigkeit seiner wissenschaftlichen Arbeiten gewürdigt wird, kann man wohl mit Recht sagen, dass er am Johanneum zu Lüneburg ein besonders günstige Konstellation angetroffen hat. Einfühlsame und kluge Lehrer förderten seine mathematische Begabung und halfen ihm, seine Schwächen so bewältigen, dass die dahinter verborgen ungewöhnlichen Stärken zum Tragen kommen konnten. Nach dem Abitur ging Riemann nach Göttingen und studierte ein Semester Theologie, wie der Vater es wollte, konnte aber dann -sicher unter Verweis auf diese Abiturbemerkung- sich ganz der Mathematik widmen. Text des gesamten Abiturzeugnisses von Bernhard Riemann in Druckschrift | |
Riemann wissenschaftliche Entwicklung und seine überragende Bedeutung |
|
 In Göttingen hörte Riemann Vorlesungen bei dem schon fast 70-jährigen Carl Friedrich Gauß über die Methode der kleinsten Quadrate. Da ihn die wenigen Vorlesungen, die Gauß noch hielt, nicht ausfüllten, führte er sein Studium in Berlin weiter, wo er die damals modernste Mathematik lernte. Er beschäftigte sich auch mit naturphilosophischen Fragen und legte 1850 seine Gedanken über eine einheitliche mathematisch-physikalische Naturauffassung in einem Aufsatz dar, in dem er forderte, "eine vollkommen in sich abgeschlossene mathematische Theorie [...], welche von den für die einzelnen Punkte geltenden Elementargesetzen bis zu den Vorgängen in dem uns wirklich gegebenen continuierlich erfüllten Raume fortschreitet, ohne zu scheiden, ob es sich um die Schwerkraft, oder die Electricität, oder den Magnetismus, oder das Gleichgewicht der Wärme handelt". Diese Forschungsrichtung im 19. Jahrhundert von Maxwell, Helmholtz und Hertz aufgegriffen und sie führte schließlich im 20. Jahrhundert zum Versuch einer allgemeinen Feldtheorie von Albert Einstein. Hier ist immernoch eine große offene Frage, wie bei Steven Hawking zu lesen ist.
 Für seine seine Promotion und Habilitation kehrte Riemann wieder nach Göttingen zum "großen Gauß" , dem "Fürst der Mathematiker" wie Daniel Kehlmann 2005 [Keh] schreibt, zurück.
Im Dezember 1851 konnte Riemann seine von Gauß hoch anerkannten Doktordissertation "Grundlagen für eine allgemeine Theorie der Funktionen einer veränderlichen komplexen Größe" abschließen. Seine Habilitationsschrift 1854 "Über die Darstellbarkeit einer Funktion durch willkürliche Funktionen" enthält nicht nur die Fourierreihen, ohne die u.a. elektronische Musik undenkbar ist, sondern das Riemannsche Integral, ohne dessen Kenntnis heutzutage niemand Abitur machen kann. Riemanns Habilitationsvortrag 1854 enthielt neue abstakte Fundierung der Geometrie, die ihm einen bleibenden Platz nicht nur unter den Mathematikern, sondern auch unter den Wegbereitern der wissenschaftlichen Weltanschauung sicherten. Seine Untersuchungen über das Vorhandensein von Ursachen für die objektiv realen Maßverhältnisse und seine Forderung, die physikalische Forschung in diese Richtung zu orientieren, wird als eine der genialsten naturwissenschftlichen Leistungen des 19. Jahrhunderts anerkannt. Sie gingen schließlich bei Albert Einstein in die Grundlagen der allgemeinen Relativitätstheorie ein. Jürgen Neffe [Nef S.242] schreibt im Einsteinjahr 2005 in seiner Einsteinbiographie: Riemanns "metrischer Tensor ist genau das was Einstein jetzt braucht". Nach dem Tod Lejeune Dirichlets, des Nachfolgers von Gauß in Göttingen, wurde Riemann 1859 zum ordentlichen Professor auf den Lehrstuhl berufen, den Gauß vier Jahre zuvor noch innegehabt hatte. Nun wurde ihm die gebührende Anerkennung zuteil und die Berliner Akademie der Wissenschaften wählte ihn zum korrespondierenden Mitglied der physikalisch-mathematischen Klasse. Riemanns Arbeiten sowie weitere Abhandlungen gaben Anlaß zu Ehrungen durch die Pariser Académie und die Londoner Royal Society. Die Zahl der von Riemann zu Lebzeiten publizierten und aus dem Nachlass herausgegebenen Arbeiten ist relativ klein. Und doch haben sie durch die Reichweite und Ideenfülle die Entwicklung der modernen Mathematik in vielfältiger Weise gefördert. Genannt seien nur einige im Brockhaus von 1992 enthaltene Stichworte: Riemannsche Flächen, Riemannsche Zahlenkugel, Riemannscher Abbildungssatz, Riemannsches Integral, Riemannsche Zetafunktion, Riemannsche Vermutung, Riemann-Geometrie, Riemannscher Raum, Riemannscher Krümmungstensor. Charakteristisch für Riemann ist, daß er viele mathematische Begriffe auf exakte, heute noch tragfähige Grundlagen stellte. Damit prägte er auch wesentlich den Stil der Mathematik und der theoretischen Physik. Aus dem Gedankenaustausch mit den Berliner Mathematikern seiner Studienzeit ging Riemanns Abhandlung "Über die Anzahl der Primzahlen unter einer gegebenen Größe" hervor. Seine Vermutungen über die Verteilung der Primzahlen sind bis heute weder bewiesen noch widerlegt. Als der hervorragende deutsche Mathematiker David Hilbert gefragt wurde, wonach er sich zuerst erkundigen würde, wenn er 100 Jahre nach seinem Tod noch einmal mit Mathematikern zusammentreffen könnte, soll er geantwortet haben: "Danach, ob die Riemannsche Vermutung bewiesen ist." Von den 23 ungelösten mathematischen Problemen, die Hilbert im Jahr 1900 benannte, ist im Jahr 2000 allein die Riemannsche Vermutung noch immer ein offenes Problem. Sie gehört daher zu den "Unsolved Seven Problems", die die Mathematiker als die Herausforderungen für des neue Jahrtausend ansehen. | |
Riemanns privates Leben und sein Tod |
|
 Sein Leben war schwer: Die Mutter hatte er früh verloren. 1855 starben der Vater und eine Schwester. Sein in Bremen als Postsekretär lebender Bruder musste für die drei anderen Schwestern aufkommen, denn Riemann verdiente als Privatdozent viel zu wenig. Seine ohnedies schon schwächliche Gesundheit hatte unter den übermäßigen geistigen Anstrengungen so gelitten, daß eine längere Erholungsreise notwendig wurde, nach deren Rückkehr er endlich zum außerordentlichen Professor mit einem Jahresgehalt von 300 Talern ernannt wurde. Als auch der Bruder und eine weitere Schwester 1857 starben, zogen die beiden verbleibenden Schwestern zu ihm nach Göttingen. Die in der Familie grassierende Krankheit war die Schwindsucht (Tuberkulose), der auch er später zum Opfer fiel.
Im Jahre 1862 befand sich Riemann auf dem Höhepunkt seines wissenschaftlichen Schaffens. In diesem Jahr heiratete er Elise Koch, eine Freundin seiner Schwester. Das Glück wurde bald getrübt: Riemann zog sich eine Brustfellentzündung zu, die nicht richtig ausheilte, obwohl er den Winter mit seiner Frau in Messina verbrachte. Auf der Rückfahrt durch Italien besuchte das Ehepaar die berühmten Kunstschätze in Neapel, Rom, Livorno, Florenz. Bologna und Mailand. Dabei machte Riemann auch die Bekanntschaft der bedeutendsten Gelehrten Italiens. Insbesondere schloß er Freundschaft mit dem Mathematiker E. Betti. Beim Übergang über die Alpen zog er sich eine neue schwere Erkältung zu, die ihn zwang, im Sommer 1863 erneut nach Italien zu reisen. Seine italienischen Freunde verschafften ihm das Angebot einer Berufung nach Pisa, die er aber ablehnte, aus Furcht, wegen seiner Krankheit die Vorlesungen nicht halten zu können. Obwohl sein Gesundheitszustand sich weiter verschlechterte, kehrte er im Herbst 1865 nach Göttingen zurück. Im Winter konnte er täglich einige Stunden arbeiten. Er vollendete noch die Abhandlung über die Theta-Funktionen. Andere Studien mußten abgebrochen werden. Trotz des Krieges zwischen Österreich und Preußen, der die Reise beschwerlich machte, begab sich Riemann im Juni 1866 auf seine dritte Reise nach Italien. Sein Befinden verschlechterte sich rasch, und schon wenige Wochen nach seiner Ankunft am Lago Maggiore verstarb er am 20. Juli 1866, in voller Gewißheit über seinen unmittelbar bevorstehenden Tod und bis zum Schluß an seinen mathematischen Untersuchungen arbeitend. | |
Literatur: |
|
| |
|
[Analysis]
[Integrale]
[Reihen]
[Geschichte der Mathematik]
| |||
 Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn Sept 96, update | |||
|
Bernhard Riemann, Leben und Wirken 
vorgetragene Version, Handzettel