www.mathematik-verstehen.de
[Komplexe Zahlen] [Algebra] [Aufbau des Zahlsystems] [Analysis [Cardano] [Geschichte] [MuPAD] [GeoGebra] [Didaktik]
| Darstellung, Gitterverbiegung | Wird einer komplexen Zahl z eine komplexe Zahl w=f(z) zugeordnet, so kann man das nicht so einfach visualisieren, da man Dimension 4 bräuchte.Wenn man nur die Bilder darstellt,reicht zwar die Gaußsche Zahleneebene aus, aber sie ist i.a. ungeliedert voller Bildpunkte. Man nimmt nun als Urbilder Gitter oder andere zu der Funktion passende Figuren wie etwa Kreise, Strahlen u.s.w. und betrachtet dann in der Gaußschen Zahlenebene, was die Funktion daraus macht. Man legt also Urbildebene und Bildebene übereinander. Die CAS haben hierfür direkte Befehle, in MuPAD plot::Conform(f(z),...). "Conform" heißt es, weil diese Art der Darstellung für winkeltreue (= "konforme") Abbbildungen sinnvoll ist. Ein Satz der Funktionentheorie -wie dieses Gebiet heißt- besagt, dass die stetig differenzierbaren Abbildungen genau die konformen sind. Insbesondere werden also rechteckige Gitter von den üblichen Funktionen so verbogen, dass im Bild die verbogenen Linien auch senkrecht aufeinander stehen. (siehe oben) |
|
| Quadrat-Fkt. | 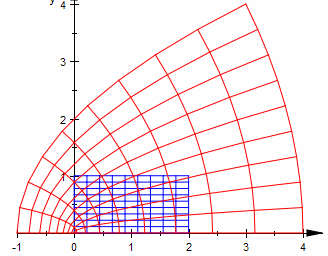 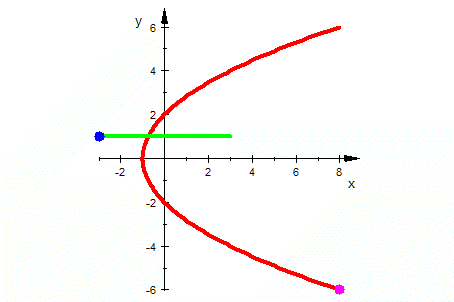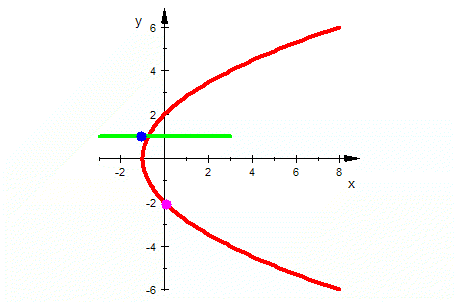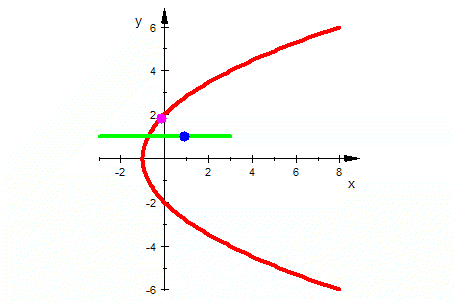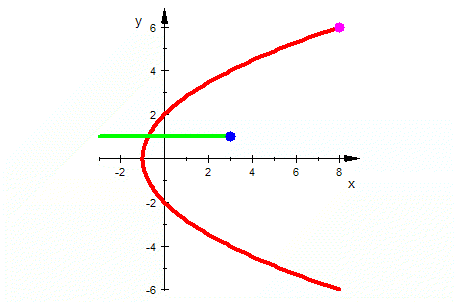 |
|
| Wurzel-Fkt. | 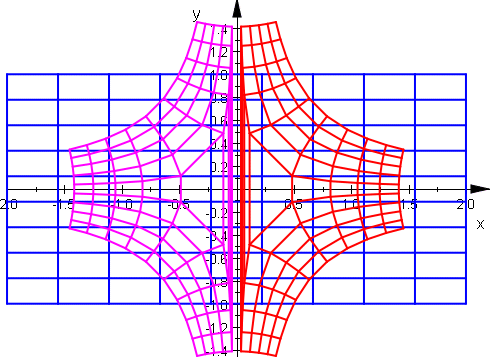 Die Kurven unter der x-Achse kommen durch Urbilder auf dem 2. Blatt der Riemannschen Fläche zustande.
Die Kurven unter der x-Achse kommen durch Urbilder auf dem 2. Blatt der Riemannschen Fläche zustande.Wurzeln aus Zahlen mit positivem Imaginäteil sind rot, aus negativem Imaginärteil sind lila. 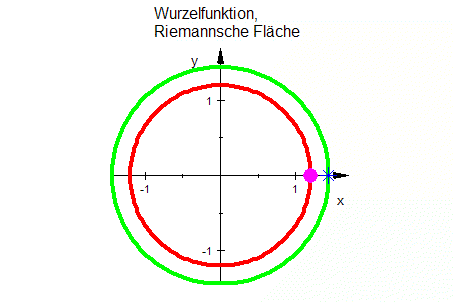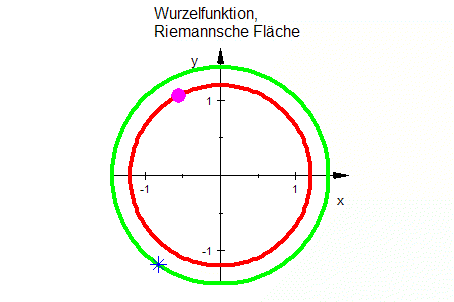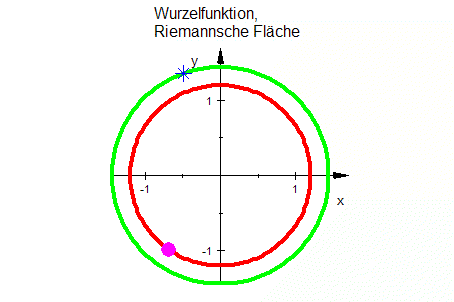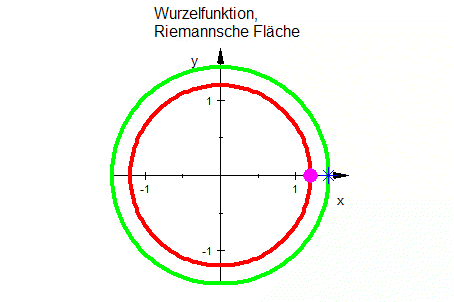 |
|
| Riemannsche Flächen | 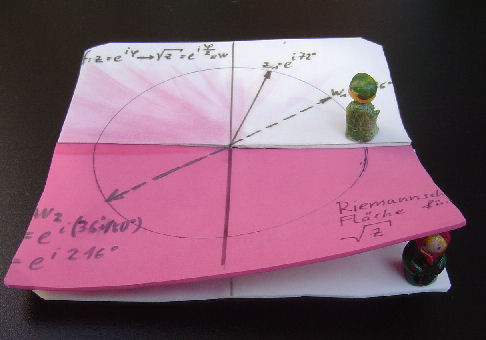 Bild aus der Präsentation zu Riemann Beschrieben auf den Seiten: Erklärungen und Rechnungen zu Quadratfkt. und Wurzelfkt. Bei Wurzel und Logarithmus passiert das erneute Durchlaufen des Kreises auf dem nächsten Blatt der Riemanschen Fläche. |
|
| Exponentialfunktion |  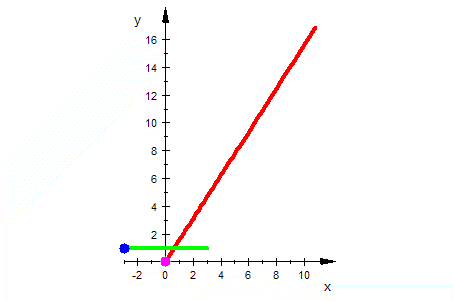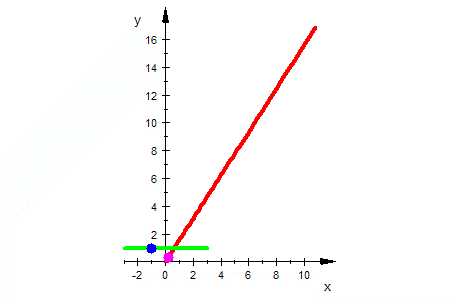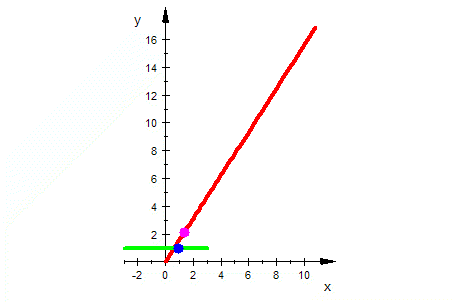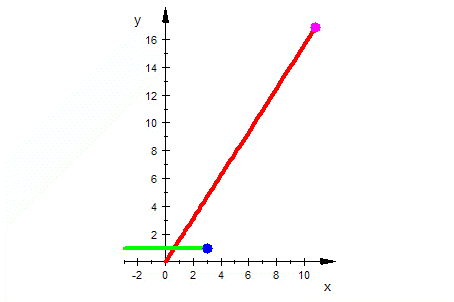 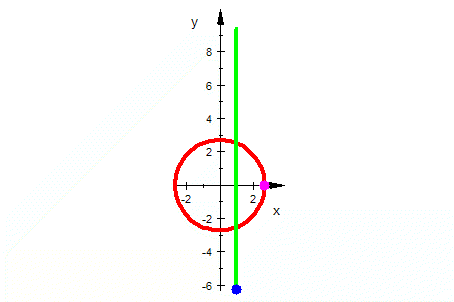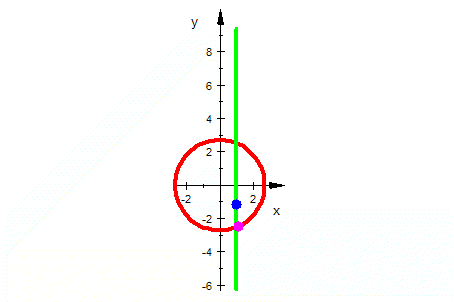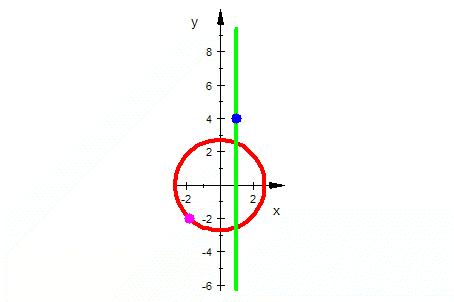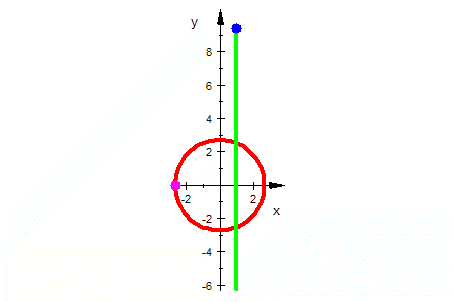 |
|
| Logarithmus-Fkt. |   |
|
| Mandelbrot Iteration |
 Mehr zum Apfelmännchen |
|
| Newton-Iteration | Newtonverfahen im Reellen steht bei den Nullstellenverfahen
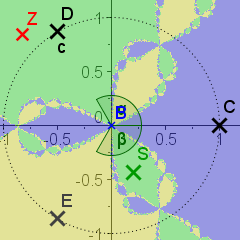
Das Newtonverfahren zur Berechnung von Nullstellen verhält sich im Komplexen in gewissen Gebieten chaotisch. Gezeigt wird der Fall für die 3. Einheitswurzeln. Ausfühliche Seite dazu und zu den anderen Einheitswurzeln ist in meiner "Ing-mathe-Formelsammlung (pdf noch nicht gelungen) |
|
| Einheitswurzeln |  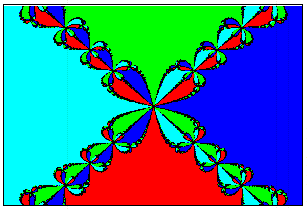      |
|
| Juliamenge |   |
|
|