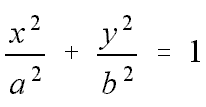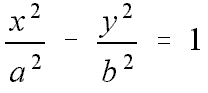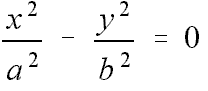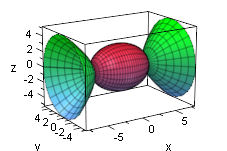
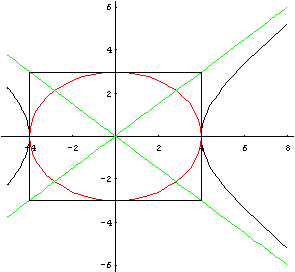Harmonie der Kegelschnitte
Volumina ihrer Rotationskörper

Diese Seite als

Gadacht als Aufgabe zur freien Erkundung

Ziel Speichern unter...


	Die Kegelschnitte haben nicht nur alle fast dieselben Gleichungen, sondern ihre Rotationskörper enthalten alle einen gemeinsamen "Volumenbausstein", dessen Vielfache die Volumina und die Zwischenräume zwischen Ihnen genau ausfüllen. Dabei wird vom Hyperboloid nur die Breite entsprechend der Halbache a betrachtet. Aufgabe zum freien Erkunden Voraussetzung: Volumenbestimmeung von um die x-Achse rotierenden Korpern durch Integration.
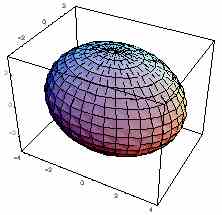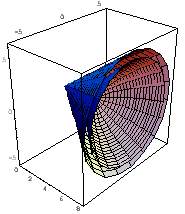
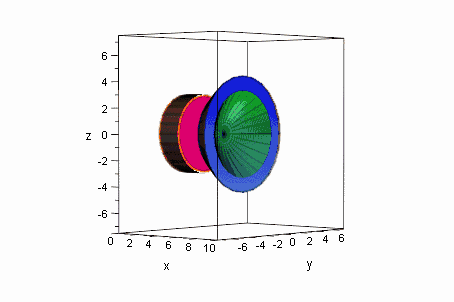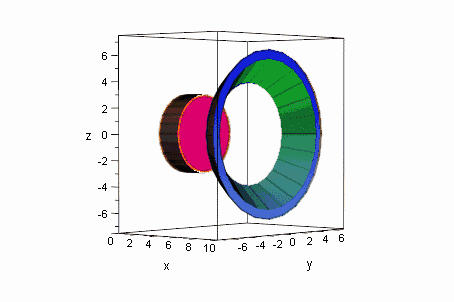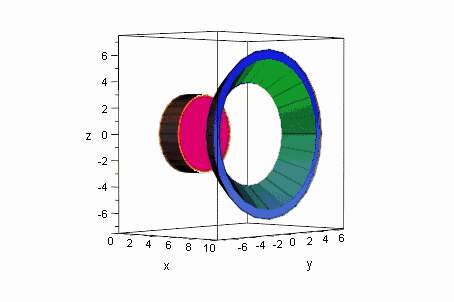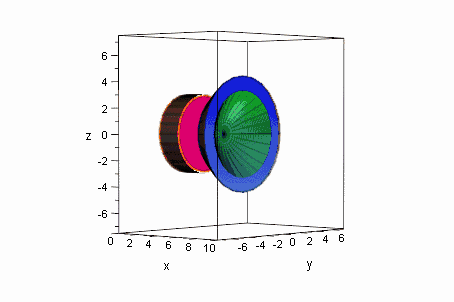
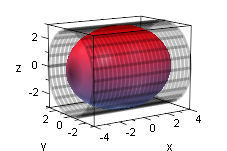
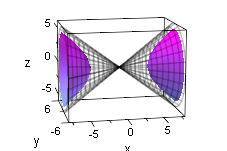
	Das Rotationsellipsoid, der darum genau passende Zylinder, die Hyberboloidschale mit der Breite a (in x-Richtung), der Kegel der Höhe 2a aus den Asymptoten und der Körper zwischen dem Kegel und der Hyperboloidschale haben Volumina, die sich aus diesen Baustein ergeben: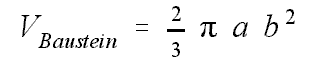 Erkunden Sie die Zusammenhänge.
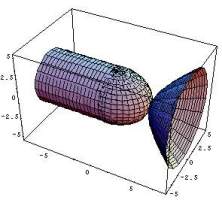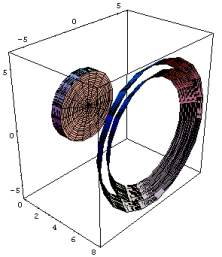
	Der Zylinder ist in dem Bild links erst halb über das Ellipsoid geschoben. Rechts ist aus dem Kegel der Asymptoten und der Hyperboloidschale ein Ring der Breite d (in x-Richtung) gebildet. Zeigen Sie, daß er dasselbe Volumen hat, wie eine Zylinderscheibe der Dicke d. Dieses Ergebnis ist unabhängig von der Stellung des Ringes!!! Animiert unten. Dr. Dörte Haftendorn, 1995