[Kurven] [Kegelschnitte] [Mathematik der Griechen]
| www.mathematik-verstehen.de | |||
[Kurven] [Kegelschnitte] [Mathematik der Griechen] | |||
| Dandelin | Germinal Pierre, französisch-belgischer
Mathematiker und Physiker, geb. 12.4.1794 Le
Bourget (bei Paris), gest. 15.2.1847 Brüssel. Nach einem Studium in Gent und Paris lehrte
Dandelin von 1825 bis 1830 Bergbauingenieurwesen
in Liège. Danach diente er in der belgischen Armee,
lehrte Physik am Athenaeo in Namur und war
Ingenieur-Oberst in Liège und später in Brüssel.
Der Begriff der Dandelinschen Kugeln geht auf ihn zurück. Dandelin bewies, daß die Berührungspunkte der Kugeln mit der Ebene gerade die Brennpunkte des Kegelschnittes der Ebene mit dem Kegel sind. Er erweiterte dieses Resultat für allgemeine Rotationsflächen. Damit konnte er 1826 den Pascalschen Satz über Sehnensechsecke von Kegelschnitten bzw. das Dual, den Satz von Brianchon über Tangentensechsecke an Kegelschnitten beweisen. 1823 veröffentlichte er ein Verfahren zur näherungsweisen Berechnung der Wurzeln einer algebraischen Gleichung n-ten Grades, das Dandelin- Gräffin-Verfahren. |
Zylinderschnitt, Ellipsen |
Kegelschnitt, Ellipsen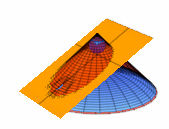 |
Kegelschnitt, Parabeln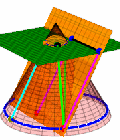 |
| ||
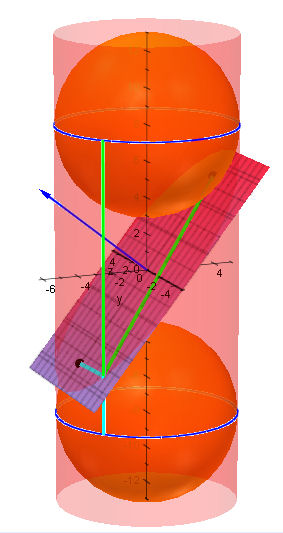 |
Es gibt eine animierte Version (2 MB)
Erklärung und BeweisDie grün-blaue Stange auf dem Zylindermantel ist überall gleichlang. Die Punkte, an denen die Kugeln die Ebene Berühren sollen Foben und Funten heißen Der Punkt, an dem die Stange die schräge Ebene durchstößt, der Punkt heiße P, ist vom oberen Berührkreis und von Foben gleich weit entfernt, wie man sich leicht überlegt. Ebeenso ist er vom unteren Berührkreis und von Funten gleich weit entfernt. Nun ist die grün-weiße Stange auch auf der Ebene zu sehen, also ist die Summe der Entfernungen von P von Foben und Funten konstant. Diese Aussage ist gerade sie Fadenkonstuktion der Ellipse. Also handelt es sich um eine bei der Schnittkurve um eine Ellipse. Schneidet man also eine Salami-Wurst, so sind die Scheiben nicht nur irgendwie oval, sondern sie sind wirkliche Ellipsen. Daher bekommen meine meine Studis am letzten Semestertag bei mir "Ellipsen-Salami". Siehe Einladung |
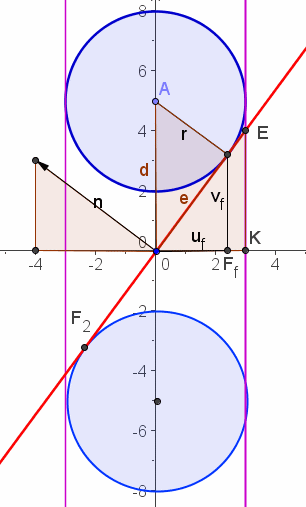 |
|
 Sinuswurst SinuswurstDie untere gerade Kante hat die Länge 2*Pi*r. Als Parameterdarstellung des geraden Schnitt-Kreises eignet sich: x= r cos( phi/r), y= r sin( phi/r), wenn nämlich der am Rand der Wurst durchlaufene Weg 2 Pi r ist, haben diese beiden Winkelfunktionen gerade eine Periode durchlaufen. Die Parameterdarstellung von z kann man der obigen Zeichung entnehmen, die Gerade hat die Gleichung z=e/r x+ c, also z= e/r r cos( phi/r) +c= e cos(phi/r) +c. Setzt man den Ursprung um Pi/2 r nach links ergibt sich z= e sin(phi/r) +c. | |
 |
| Es gibt eine animierte Version (2 MB)
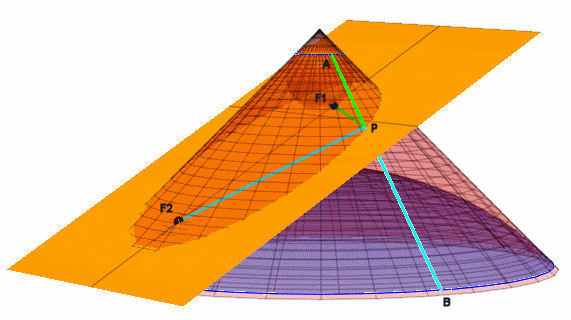
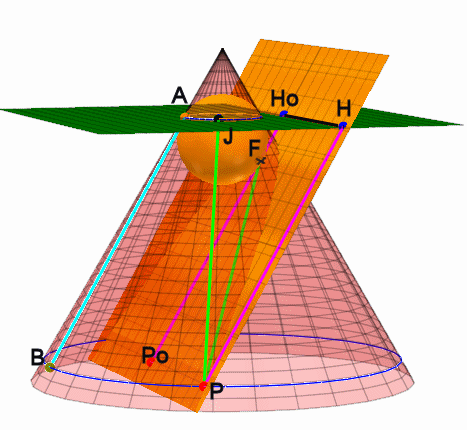
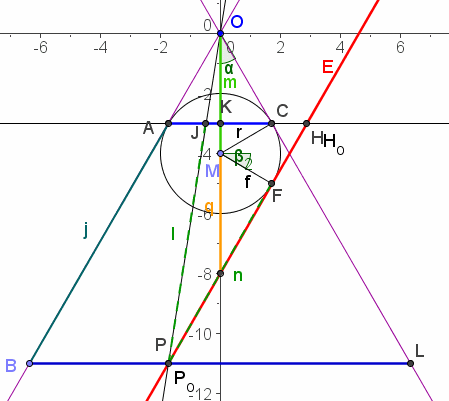
Erklärung und Beweis Die grün-blaue Stange auf dem Kegelmantel ist überall gleichlang. Die Punkte, an denen die Kugeln die Ebene Berühren sollen Foben und Funten heißen Der Punkt, an dem die Stange die schräge Ebene durchstößt, der Punkt heiße P, ist vom oberen Berührkreis und von Foben gleich weit entfernt, wie man sich leicht überlegt. Ebeenso ist er vom unteren Berührkreis und von Funten gleich weit entfernt. Nun ist die grün-weiße Stange auch auf der Ebene zu sehen, also ist die Summe der Entfernungen von P von Foben und Funten konstant. Diese Aussage ist gerade sie Fadenkonstuktion der Ellipse. Also handelt es sich um eine bei der Schnittkurve um eine Ellipse. Schneidet man also einen Kegel, so sind die Schnittränder nicht nur irgendwie oval, sondern sie sind wirkliche Ellipsen. Daher bekommen meine meine Studis am letzten Semestertag bei mir "Kegelschnittkuchen". Siehe Einladung |
|
animierte Version (2 MB) |
 |
|  |
http://haftendorn.uni-lueneburg.de http://mathematik.uni-lueneburg.de |