http://haftendorn.uni-lueneburg.de/mathe-lehramt/kurven/kegel/kegel.htm[Kurven] [Kegelschnitte] [Dandelinsche Kugeln] [Mathematik der Griechen]
 |
|
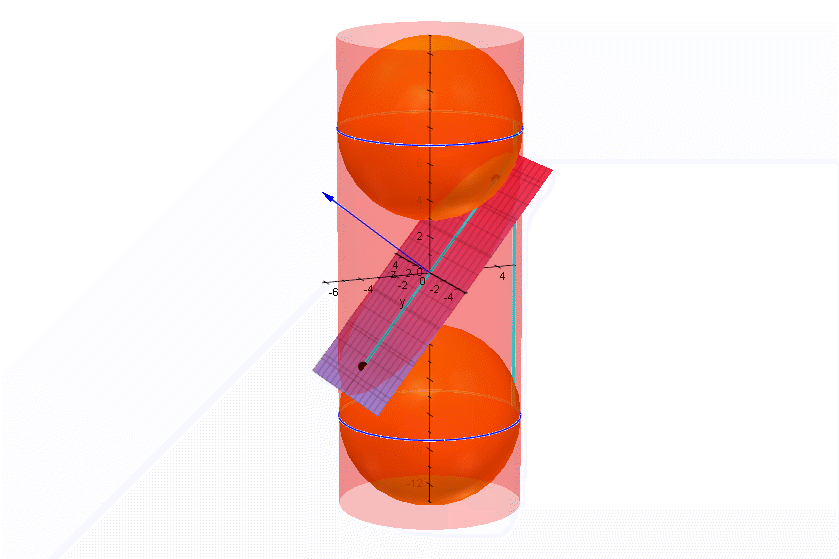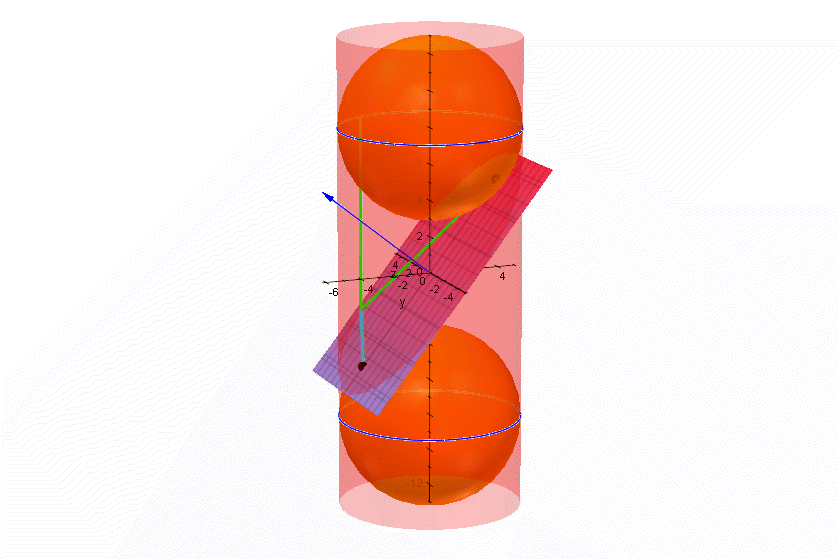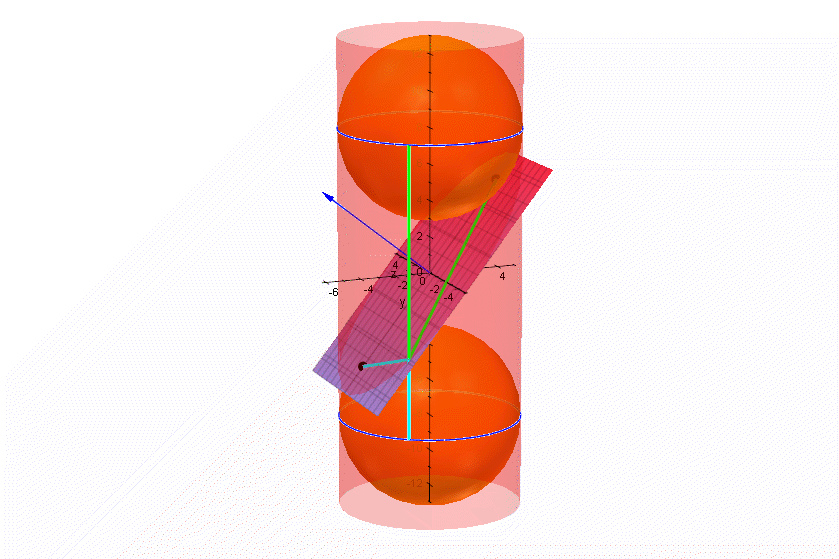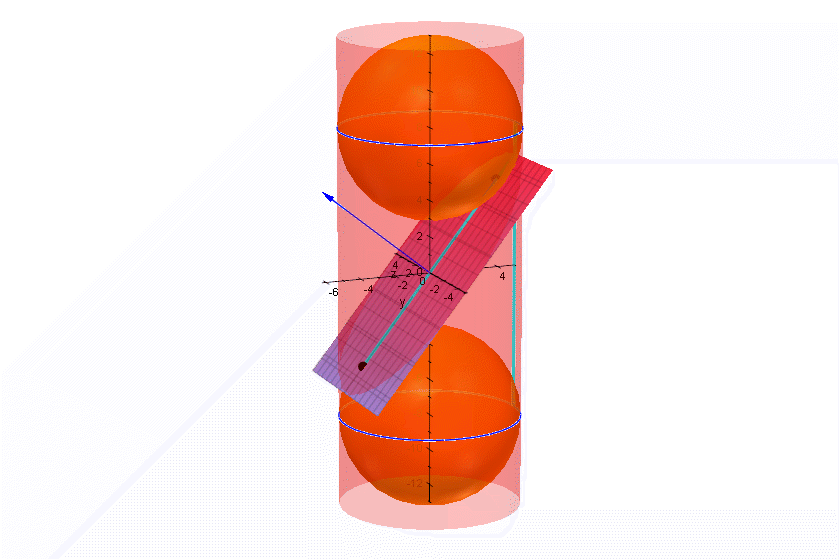
| Die grün-blaue Stange auf dem Zylindermantel ist überall gleichlang. Die Punkte, an denen die Kugeln die Ebene berühren, sollen Foben und Funten heißen Der Punkt, er heiße P, an dem die Stange die schräge Ebene durchstößt, ist vom oberen Berührkreis und von Foben gleich weit entfernt, wie man sich leicht überlegt. Ebenso ist er vom unteren Berührkreis und von Funten gleich weit entfernt. Nun ist die grün-hellblaue Stange auch auf der Ebene zu sehen, also ist die Summe der Entfernungen von P von Foben und Funten konstant. Diese Aussage ist gerade sie Fadenkonstuktion der Ellipse. Also handelt es sich bei der Schnittkurve um eine Ellipse. Schneidet man also eine Salami-Wurst, so sind die Scheiben nicht nur irgendwie oval, sondern sie sind wirkliche Ellipsen. Daher bekommen meine Studis am letzten Semestertag bei mir "Ellipsen-Salami". Siehe Einladung | |
|
[Kurven]
[Kegelschnitte]
[Dandelinsche Kugeln]
[Mathematik der Griechen]
|
 Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn Nov. 2003, update |
 www.mathematik-verstehen.de www.doerte-haftendorn.dehttp://haftendorn.uni-lueneburg.de http://mathematik.uni-lueneburg.de |