www.mathematik-verstehen.de
Link zum Buch
[] [Regression] [Computer]
www.mathematik-verstehen.de |
| Link zum Buch |
|
URL http://haftendorn.uni-lueneburg.de/mathe-lehramt/stochastik/stochastik.htm [] [Regression] [Computer] | ||
Statistik,
Formeln für VarianzenEs geht im Folgenden um die Abweichungen vom Datenschwerpunkt.![]()
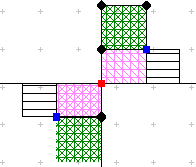 Kovarianz:
Kovarianz: ![]()
Dies kann man als mittleres Abweichungsrechteck auffassen.
x-Varianz
Dies kann man als mittleres Abweichungsquadrat in x-Richtung auffassen.
x-Standardabweichung
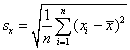 ist demnach die Kantenlänge dieses mittleren x-Abweichungsquadrates.
ist demnach die Kantenlänge dieses mittleren x-Abweichungsquadrates.
y-Varianz
Das kann man als mittleres Abweichungsquadrat in y-Richtung auffassen.
y-Standardabweichung

ist demnach die Kantenlänge dieses mittleren y-Abweichungsquadrates.
Damit das Produkt ![]() auffassbar als Kantenlänge eines Rechtecks, das aus den beiden mittleren Abweichungsquadraten gebildet werden kann.
auffassbar als Kantenlänge eines Rechtecks, das aus den beiden mittleren Abweichungsquadraten gebildet werden kann.
In dem oben dargestellten Sonderfall ist dieses Rechteck dasselbe, das auch durch die Kovarianz beschrieben wird. Damit ist der Quotient aus beiden im obigen Fall 1, ebenso in anderen Fällen. In denen die Daten auf einer Geraden liegen. Sonst ist er kleiner 1.
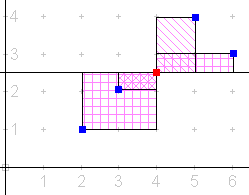 Man kann sich vorstellen, dass durch die Quotientenbildung eine Normierung vorgenommen wird. Dadurch entsteht eine Messgröße, die die Abweichung der Daten von einer Geraden sinnvoll beschreiben kann.
Man kann sich vorstellen, dass durch die Quotientenbildung eine Normierung vorgenommen wird. Dadurch entsteht eine Messgröße, die die Abweichung der Daten von einer Geraden sinnvoll beschreiben kann.
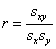 , der Koorelationskoeffizient.
, der Koorelationskoeffizient. ![]()
Interaktive Version (Euklid Dynageo ActiveX, Internet Explorer >4)
Beweise für die alternativen Berechnungsformeln:
|
|
Ebenso
Beachte dabei
|
Fast ebenso
|
www.mathematik-verstehen.de |
[Stochastik]
[Regression]
[Computer] Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn |
Link zum Buch |
| www.leuphana.de/matheomnibus www.doerte-haftendorn.de http://haftendorn.uni-lueneburg.de http://www.mathematik-sehen-und-verstehen.de |